Satz des Pythagoras Erklärung mit Beispiel

Kann man den Satz des Pythagoras so einfach erklären, dass jeder ihn versteht? Wir versuchen es hier. Stellt euch vor ein Schüler kommt nach der Schule zu seiner Oma und versucht ihr zu erklären, wie der Satz des Pythagoras funktioniert. Glaubt ihr eine echte Oma würde die folgenden Erklärungen verstehen?

Enkel: Das haben wir heute in der Schule gemacht. Der Lehrer wollte, dass wie die längste Seite in einem Dreieck berechnen. Weißt du noch wie das geht?

Oma: Keine Ahnung. Viel zu lange her. Erklär es mir mal.

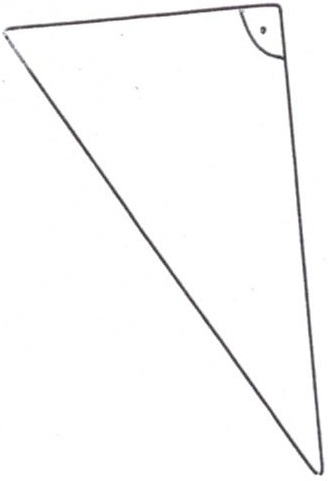
Enkel: Wir haben das mit dem Satz des Pythagoras gemacht. Wichtig ist, dass man diesen nur nutzen darf, wenn es einen rechten Winkel im Dreieck gibt. Ein rechter Winkel ist so groß wie wenn der Stundenzeiger einer Uhr sich um drei Stunden gedreht hat. Das ist so viel wie die Ecke mit dem Punkt und dem Viertelkreis im nächsten Bild.

Formel Satz des Pythagoras

Oma: Verstehe. Und wenn ich das habe kann ich was machen?

Enkel: Wenn wir das haben können wir die längste Seite im Dreieck berechnen. Diese bezeichnet man als Hypotenuse und sie liegt gegenüber vom rechten Winkel. Die beiden anderen Seiten vom Dreieck nennt man Katheten. Die Formel lautet a zum Quadrat plus b zum Quadrat gleich c zum Quadrat.

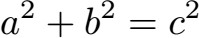
Oma: Das verstehe ich nicht. Was sind denn a, b oder c?

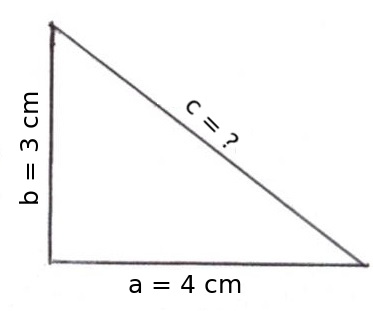
Enkel: Das c ist die Länge der längsten Seite und a sowie b sind die Längen der beiden Katheten (also der kürzeren Seiten). Ich mache mal ein Beispiel: Wir haben die Längen der Katheten mit b = 3 cm und a = 4 cm. Die beiden kürzeren Seiten im Dreieck sind 3 cm und 4 cm lang.

Anzeigen:

Hypotenuse berechnen

Oma: Aha. Wenn ich dies weiß kann ich damit die Länge c berechnen?

Enkel: Genau. Wir setzen dies in unsere Formel oder Gleichung ein. Für a setzen wir die 4 cm ein und für b die 3 cm.

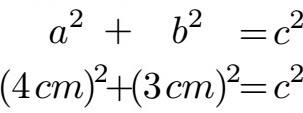
Oma: Was sollen die Klammern um die 4 cm und 3 cm?

Enkel: Wir müssen beide Angaben quadrieren. Das erkennt man an der kleinen 2 über a und über b. Quadrieren heißt wir müssen beide Längenangaben mit sich selbst multiplizieren.

Oma: Mach mal vor und erkläre es mir.

Enkel: Schau mal auf die Rechnung:

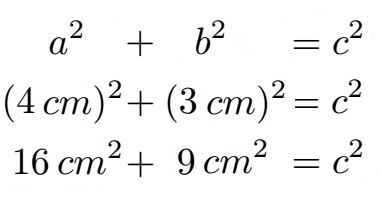
Enkel: Wir müssen die Länge von 4 cm mit sich selbst multiplizieren. Da haben wir 4 · 4 = 16. Auch die Zentimeter (cm) müssen wir mit sich selbst multiplizieren. Aus cm mal cm wird Zentimeter zum Quadrat, also cm². Bei den 3 cm genauso: Wir bekommen als Zahl 3 · 3 = 9 und cm · cm = cm².

Wurzel ziehen Mathematik

Oma: Und wie lange ist nun die dritte Seite vom Dreieck?

Enkel: Dazu rechnen wir 16 cm² + 9 cm² = 25 cm². Der Mathematik-Lehrer nennt dies Addition. Im Anschluss müssen wir die Wurzel ziehen.

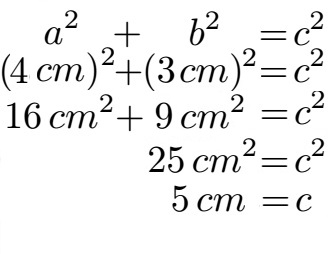
Oma: Wurzel ziehen? Ich kenne Wurzelbehandlung vom Zahnarzt. Das tut richtig weh.

Enkel: Meine Tischnachbarin sah auch so aus als tat ihr das Wurzel ziehen weh. Aber es ist nur Mathematik. Man kann das Ziehen der Wurzel mit dem Taschenrechner machen oder bei so einfachen Aufgaben auch im Kopf. Dabei ist die Wurzel aus 25 einfach 5, denn 5 · 5 = 25. Die Wurzel aus cm² ist wieder cm, denn umgekehrt war vorhin cm · cm = cm². Wurzel ziehen ist damit die Umkehrung vom Quadrat (hoch 2) von vorhin.

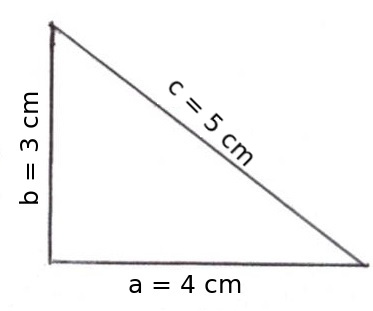
Oma: Das heißt die längste Seite im Dreieck ist c mit einer Länge von 5 cm?

Enkel: So ist es.

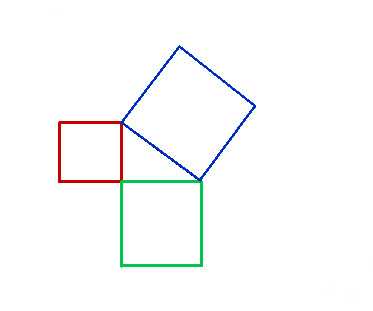
Enkel: Man kann sich den Satz des Pythagoras auch grafisch vorstellen. Dazu erweitert man jede Seite vom Dreieck zu einem Quadrat. Die Fläche vom roten Quadrat plus der Fläche vom grünen Quadrat ist so groß wie die Fläche vom blauen Quadrat. Daraus ergibt sich auch die Formel a² + b² = c².

Aufgaben Satz des Pythagoras

Aufgabe 1: Glaubt ihr das Thema Satz des Pythagoras verstanden zu haben? Möchtet ihr das Thema ein bisschen üben? Wir bieten euch hier die Möglichkeit Aufgaben zu rechnen und sich die Lösung dabei anzusehen. Da viele Schüler jedoch schon bei den Begriffen scheitern, fangen wir mit einfachen Fragen dazu an. Fragen und Aufgaben können per Klick übersprungen werden.

• Wie nennt man die längste Seite in einem rechtwinkligen Dreieck?

• Gegenkathete
• Ankathete
• Kathete
• Hypotenuse

Weiter zur Lösung » Aufgabe überspringen »

Du hast 0 von 6 Aufgaben erfolgreich gelöst.