Brüche kürzen und erweitern

Wie kürzt oder erweitert man Brüche? Warum ändert sich der Wert eines Bruchs beim Erweitern oder Kürzen nicht? Ich versuche die Inhalte so einfach zu erklären, wie ich dies selbst bei meiner Oma (lange aus der Schule raus) tun würde. Die Inhalte liegen als Text und als Video vor.

Brüche können in der Mathematik oftmals gekürzt oder erweitert werden. In beiden Fällen ändert sich der Wert des Bruchs nicht, da Zähler und Nenner des Bruchs gleichzeitig angepasst werden. Kürzen bedeutet die Anzahl der ausgewählten Teile und gleichzeitig alle Teile zu reduzieren. Zum Beispiel werden 5 von 10 Teile auf 1 von 2 Teile reduziert.

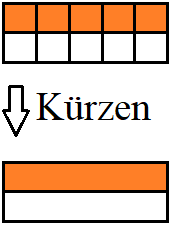
Umgekehrt können Brüche erweitert werden. Dabei wird zum Beispiel ein Streifen in mehr Teile unterteilt, jedoch auch mehr Teile ausgewählt. Im nächsten Beispiel wird 1 von 2 auf 5 von 10 erweitert.

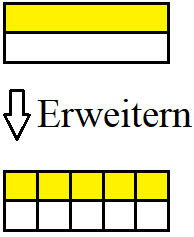
Oft kommt dabei die Frage: "Warum ändert sich der Wert eines Bruches beim Erweitern oder Kürzen nicht?" Dies liegt daran, dass sowohl die Anzahl der ausgewählten Teile als auch der Gesamtzahl aller Teile im gleichen Maße erweitert wird.

Wie kürzt und erweitert man Brüche?

Brüche werden gekürzt, indem Zähler und Nenner durch die gleiche Zahl geteilt werden. Brüche werden erweitert, indem Zähler und Nenner mit der gleichen Zahl multipliziert werden. Im nächsten Beispiel wird der Bruch mit 2 gekürzt.

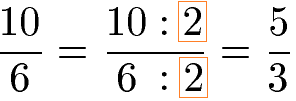
Ein sinnvolles kürzen erfordert es Zähler und Nenner durch die gleiche natürliche Zahl (1, 2, 3, 4, ...) zu teilen ohne das im Zähler oder Nenner eine Dezimalzahl (Kommazahl) entsteht. Im nächsten Beispiel lässt sich die 15 nicht mit 2 kürzen. Daher versuchen wir das Kürzen des Bruchs mit der Zahl 3. Dies funktioniert, da sowohl 15 als auch 12 sich durch 3 teilen lassen.

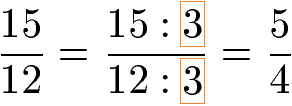
Einen Bruch mit 2 zu erweitert bedeutet den Zähler und den Nenner des Bruchs mit 2 zu multiplizieren. Das nächste Beispiel zeigt wie ein Bruch mit 3 im Zähler und 4 im Nenner mit 2 erweitert wird.

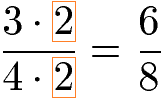
Als weiteres Beispiel soll ein Bruch mit 3 erweitert werden. Daher wird der Zähler (10) und der Nenner (4) jeweils mit 3 multipliziert.

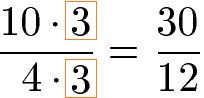
Im nächsten Abschnitt sehen wir uns eine Anwendung für das Erweitern von Brüchen an.

Anzeigen:

Wie erweitert man Brüche auf den Hauptnenner?

Um Brüche zu addieren oder zu subtrahieren müssen alle Brüche auf einen gemeinsamen Nenner gebracht werden. Es gibt verschiedene Möglichkeiten einen gemeinsamen Nenner zu berechnen.

Die einfachste Möglichkeit besteht darin alle Nenner miteinander zu multiplizieren. Als Beispiel dienen drei Brüche die subtrahiert bzw. addiert werden.

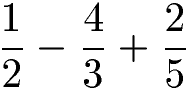
Um einen gemeinsamen Nenner zu finden multiplizieren wir die Nenner der drei Brüche.

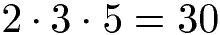
Alle Brüche müssen auf den Nenner 30 gebracht werden. Dazu erweitern wir den ersten Bruch mit 15, den zweiten Bruch mit 10 und den dritten Bruch mit 6.

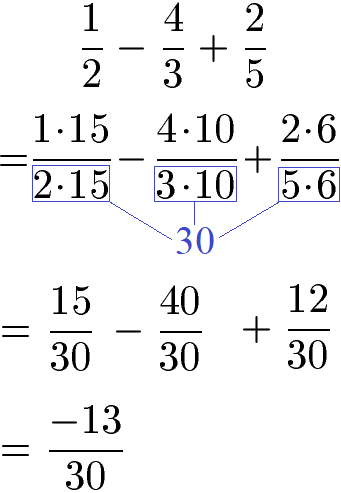
Nicht immer entsteht bei der Multiplikation aller Nenner der Hauptnenner. Der Hauptnenner ist der kleinstmögliche Nenner für alle Zahlen. Um diesen zu finden, musst du mit allen Nennern das kleinste gemeinsame Vielfache berechnen. Wie dies funktioniert lernst du unter kgV: kleinstes gemeinsames Vielfaches.