Primzahlen Beispiele und Erklärung

Was ist eine Primzahl? Wie kann ich eine Primzahl erkennen oder berechnen? Was sind die Primzahlen von 1 bis 100? Dies und mehr versuche ich in diesem Artikel zu erklären. Ich versuche alles so einfach zu erklären, wie ich dies selbst bei meiner Oma (lange aus der Schule raus) tun würde.

Eine Primzahl ist eine natürliche Zahl mit nur zwei Teilern. Diese hat folgende Eigenschaften:

• Sie kann durch 1 geteilt werden.
• Sie kann durch sich selbst geteilt werden.
• Einen weiteren Teiler gibt es nicht!

Wie kann ich eine Primzahl erkennen? Es gibt verschiedene Methoden zu erkennen, ob eine Zahl eine Primzahl ist oder nicht. Eine leicht zu verstehende Methode - welche auch schon in der Grundschule verwendet wird - besteht darin, durch alle natürlichen Zahlen zu teilen und auf einen Rest zu überprüfen.

Wie erkenne ich eine Primzahl?

Sehen wir uns eine Möglichkeit an, wie man Primzahlen erkennt. Dazu nehmen wir eine Zahl und teilen diese durch die natürlichen Zahlen bis zu dieser Zahl.

Beispiel 1: Primzahl erkennen mit der Zahl 6

Um zu überprüfen, ob die Zahl 6 eine Primzahl ist, teilen wir diese durch die Zahlen 1, 2, 3, 4, 5 und 6. In den Fällen in denen kein Rest bei der Berechnung entsteht, liegt ein Teiler vor. Wir erhalten 1, 2, 3 und 6 als Teiler.

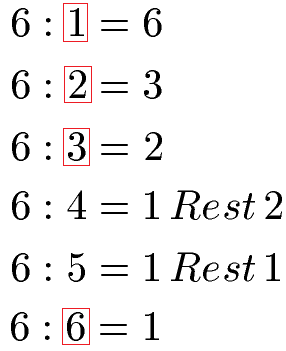
Da es neben der 1 und sich selbst (6) noch weitere Teiler gibt, ist die Zahl 6 keine Primzahl.

Beispiel 2: Primzahl erkennen mit der Zahl 7

Um zu überprüfen, ob die Zahl 7 eine Primzahl ist, teilen wir diese durch die Zahlen 1, 2, 3, 4, 5, 6 und 7. In den Fällen in denen kein Rest bei der Berechnung entsteht, liegt ein Teiler vor. Die Zahl 7 hat die Teiler 1 und 7.

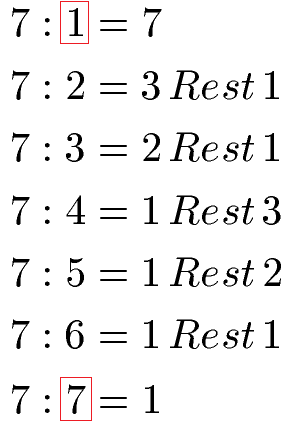
Da nur die Teiler 1 und sich selbst (7) vorliegen, sprich nur 2 Teiler, ist die Zahl 7 eine Primzahl.

Anzeigen:

Wie lauten die Primzahlen 1 bis 20, 1 bis 100 und bis 1000?

In diesem Abschnitt gibt es Listen von Primzahlen für verschiedene Zahlenräume.

Was sind die Primzahlen von 1 bis 20?

2, 3, 5, 7, 11, 13, 17, 19

Was sind die Primzahlen von 1 bis 100?

2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97

Was sind die Primzahlen von 1 bis 1000?

2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97, 101, 103, 107, 109, 113, 127, 131, 137, 139, 149, 151, 157, 163, 167, 173, 179, 181, 191, 193, 197, 199, 211, 223, 227, 229, 233, 239, 241, 251, 257, 263, 269, 271, 277, 281, 283, 293, 307, 311, 313, 317, 331, 337, 347, 349, 353, 359, 367, 373, 379, 383, 389, 397, 401, 409, 419, 421, 431, 433, 439, 443, 449, 457, 461, 463, 467, 479, 487, 491, 499, 503, 509, 521, 523, 541, 547, 557, 563, 569, 571, 577, 587, 593, 599, 601, 607, 613, 617, 619, 631, 641, 643, 647, 653, 659, 661, 673, 677, 683, 691, 701, 709, 719, 727, 733, 739, 743, 751, 757, 761, 769, 773, 787, 797, 809, 811, 821, 823, 827, 829, 839, 853, 857, 859, 863, 877, 881, 883, 887, 907, 911, 919, 929, 937, 941, 947, 953, 967, 971, 977, 983, 991, 997

In den nächsten Abschnitten geht es noch um typische Fragen zu Primzahlen. Außerdem kommt mit der Primfaktorzerlegung eine typische Anwendung für Primzahlen dran.

Primzahlen und Primfaktorzerlegung

Ist eine natürliche Zahl keine Primzahl, so kann diese in Multiplikationen aus Primzahlen zerlegt werden. Dies kann in mehreren Schritten erfolgen.

Beispiel 1: Primfaktorzerlegung am Beispiel 36

Die Zahl 36 soll vollständig in Primfaktoren zerlegt werden. Die 36 lässt sich dabei erst einmal in 6 · 6 zerlegen. Die Zahlen 6 wiederum können jeweils in 2 · 3 zerlegt werden. Sowohl die Zahl 2 als auch die Zahl 3 sind Primzahlen. Daher ist die Primfaktorzerlegung komplett.

Beispiel 2: Primfaktorzerlegung am Beispiel 64

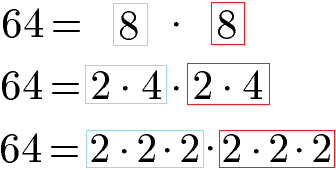
Die Zahl 64 soll vollständig in Primfaktoren zerlegt werden. Die 64 lässt sich dabei erst einmal in 8 · 8 zerlegen. Die Zahlen 8 wiederum können jeweils in 2 · 4 zerlegt werden. Und die 4 kann selbst wieder in 2 · 2 zerlegt werden. Die Zahl 2 ist eine Primzahl. Daher ist die Primfaktorzerlegung jetzt vollständig.

Weitere Beispiele zu Primzahlen

In diesem Abschnitt noch einige typische Fragen rund um Primzahlen.

Wann werden Primzahlen in der Schule behandelt?

Primzahlen werden oftmals schon in der 3. Klasse oder 4. Klasse in Mathematik behandelt. Dabei sollen Schüler die Primzahlen im Zahlenraum bis 20 oder 100 lernen. Eine Zahl wird auf eine Primzahl durch eine Division mit oder ohne Rest getestet.

Ist 1 eine Primzahl oder nicht?

Die Zahl 1 hat nur einen Teiler und dies ist die Zahl 1 selbst. Es gibt keinen zweiten Teiler. Daher hat man beschlossen die 1 nicht zu den Primzahlen zu zählen.

Warum ist die Zahl 2 eine Primzahl?

Die Zahl 2 hat zwei Teiler. Die Zahl 1 ist ein Teiler. Die Zahl 2 ist ein Teiler. Es liegen damit zwei verschiedene Teiler vor (nicht mehr) und die 2 ist dadurch eine Primzahl.

Ist die Zahl 9 eine Primzahl?

Die Zahl 9 ist keine Primzahl, denn es gibt mehr als 2 Teiler: Die 9 kann durch 1 und 9 geteilt werden. Sie kann jedoch auch durch 3 ohne Rest geteilt werden. Daher ist die Zahl 9 keine Primzahl.