Kommutativgesetz ▷ Addition, Subtraktion, Multiplikation und Division
Geschrieben von: Dennis RudolphDienstag, 23. November 2021 um 16:21 Uhr
Was ist das Kommutativgesetz? Wie funktioniert das Kommutativgesetz für Addition und Multiplikation? Kann ich dieses Rechengesetz auch für Subtraktion und Division einsetzen? Ich versuche alles so einfach zu erklären, wie ich dies selbst bei meiner Oma (lange aus der Schule raus) tun würde. Die Inhalte liegen als Text und als Video vor.
Das Kommutativgesetz (auch Vertauschungsgesetz genannt) ist ein Rechengesetz der Mathematik. Es besagt, dass man bei der Addition und Multiplikation von Zahlen die Reihenfolge der Zahlen vertauschen darf. Die Rechenarten Subtraktion und Division sind nicht kommutativ.
Warum das Kommutativgesetz funktioniert oder nicht funktioniert sehen wir uns in den nächsten Abschnitten für alle vier Grundrechenarten (Addition, Subtraktion, Multiplikation und Division) an. Beispiele weiter unten.
Wie funktioniert das Kommutativgesetz bei der Addition?
Bei einer Addition dürfen die Summanden vertauscht werden. Zur Erinnerung: Die Summanden sind die Zahlen, welche addiert werden. Und um es gleich vorweg zu nehmen: Auch mehr als zwei Summanden dürfen beliebig in der Reihenfolge vertauscht werden. Sehen wir uns dazu Beispiele an.
Gleichung Kommutativgesetz Addition:
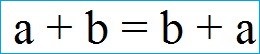
Beispiele Kommutativgesetz Addition:
Die Reihenfolge der Zahlen spielt keine Rolle. Ob 4 + 8 oder 8 + 4 gerechnet wird, die Summe ist jeweils 12.
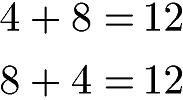
Ob 3 + 6 gerechnet wird oder 6 + 3 ergibt stets 9.
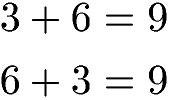
Anzeigen:
Gilt das Kommutativgesetz bei der Subtraktion?
Nein. Das Kommutativgesetz gilt bei der Subtraktion nicht! Die Zahlen bei der Subtraktion dürfen nicht vertauscht werden. In Fachworten: Minuend und Subtrahend dürfen nicht vertauscht werden. Einige Beispiele verdeutlichen dies.
Kommutativgesetz Subtraktion Ungleichung:
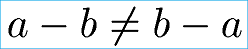
Kommutativgesetz Subtraktion Beispiele:
Werden Minuend und Subtrahend bei der Subtraktion vertauscht entsteht eine andere Differenz. So liefert 6 - 8 eine andere Differenz als 8 - 6.
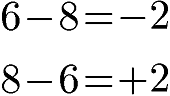
Dies gilt auch für 5 - 3 im Vergleich zu 3 - 5.
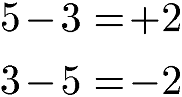
Hinweis: Wie man an den Beispielen sehen kann führt ein Vertauschen von Minuend und Subtrahend dazu, dass sich das Vorzeichen im Ergebnis ändert.
Wie lautet das Kommutativgesetz für die Multiplikation?
Bei einer Multiplikation dürfen die Faktoren vertauscht werden. Zur Erinnerung: Die Faktoren sind die Zahlen, welche multipliziert werden. Auch mehr als zwei Faktoren dürfen beliebig in der Reihenfolge vertauscht werden. Sehen wir uns auch dazu einige Beispiele an.
Gleichung Kommutativgesetz Multiplikation:
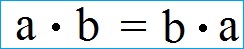
Beispiele Kommutativgesetz Multiplikation:
Die Multiplikation von 5 mit 3 oder 3 mit 5 ergibt in beiden Fällen die 15 als Produkt.
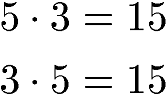
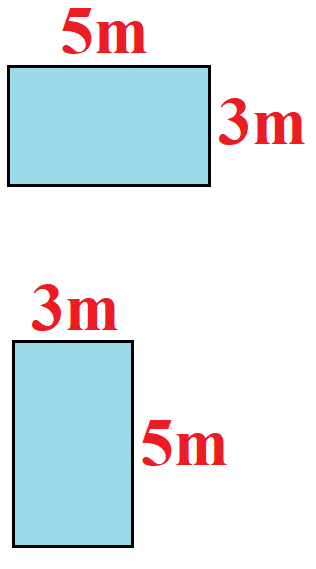
Grafisch kann man sich dies sehr schön mit Strecken und Flächen veranschaulichen. Ein Raum ist 5 Meter breit und 3 Meter lang. In diesem Fall ist die Fläche 15 Quadratmeter. Ist der Raum 5 Meter lang und 3 Meter breit ändert dies jedoch nichts an der Fläche von 15 Quadratmetern.
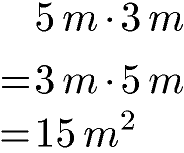
Die beiden blauen Flächen sind gleich groß.
Gilt das Kommutativgesetz bei der Division?
Nein. Das Kommutativgesetz gilt bei der Division nicht! Die Zahlen bei der Division dürfen nicht vertauscht werden. In Fachworten: Dividend und Divisor dürfen nicht vertauscht werden. Einige Beispiele zeigen wozu dies führen würde.
Kommutativgesetz Division Ungleichung:
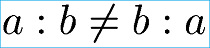
Kommutativgesetz Division Beispiele:
Wird 12 durch 3 geteilt entsteht ein anderes Ergebnis als wenn 3 durch 12 geteilt wird. Daher ist die Division nicht kommutativ.
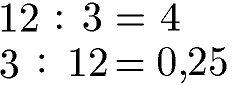
Das eben gezeigte Beispiele zur Division kann auch in Form eines Bruchs dargestellt werden. Ein Bruch ist nichts anderes als eine Division.
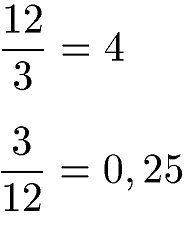
Meistgelesene Inhalte
- Allgemenbildung Quiz
- Prozentrechnung
- Bruchrechnen
- Satz des Pythagoras
- PQ-Formel
- Mitternachtsformel
- Polynomdivision
- Zinsrechnung
- Gleichungen umformen
- Nullstellen bestimmen
- Dreisatz
Neue Artikel
- Rationale Zahlen ▷ Ist eine Zahl rational?
- Bruch in Kommazahl (Dezimalzahl) umwandeln
- Koordinatensystem: Erklärung und Punkte
- Brüche kürzen und erweitern
- Brüche multiplizieren und dividieren
- Rechteck Eigenschaften: Flächeninhalt, Umfang und mehr
- Brüche addieren und subtrahieren
- Sachaufgaben Klasse 5 Mathematik
- Flächeninhalt Rechteck ▯ Beispiele + Erklärung
- Umfang Rechteck mit Formeln berechnen
