Grundrechenarten ▷ Mathe Übersicht

Die 4 Grundrechenarten der Mathematik lernst du hier. Dabei zeige ich dir wie diese Grundrechenarten heißen und welche Fachbegriffe man zu diesen kennen sollte. Ich versuche alles so einfach zu erklären, wie ich dies selbst bei meiner Oma (lange aus der Schule raus) tun würde. Die Inhalte liegen als Text und als Video vor.

Es gibt 4 Grundrechenarten in der Mathematik. Diese lauten Addition, Subtraktion, Multiplikation und Division. Ab der Grundschule werden diese Rechenarten behandelt. Auch für den Mathematik-Unterricht nach der Grundschule solltest du die Grundrechenarten wirklich beherrschen. Falls gerade nur eine bestimmte Grundrechenart für dich interessant ist, findest du diese hier auch direkt:

• Addition (Addieren)
• Subtraktion (Subtrahieren)
• Multiplikation (Multiplizieren)
• Division (Dividieren)

Grundrechenart: Was gehört zur Addition?

Zu einer Addition gehört ein Pluszeichen (+). Vor dem Pluszeichen steht der 1. Summand, nach dem Pluszeichen findet sich der 2. Summand. Das Ergebnis der Addition wird als Summe bezeichnet.

Addition bedeutet nichts anderes als "hinzufügen". Zu einer Zahl wird eine andere Zahl hinzugefügt. Sehr einfach zu verstehen ist dies an einem Zahlenstrahl. Zwei Beispiele:

• 2 + 6 = 8 bedeutet von der 2 um 6 nach rechts zu gehen und auf der 8 zu landen.
• 3 + 4 = 7 bedeutet von der 3 um 4 nach rechts zu gehen und auf der 7 zu landen.

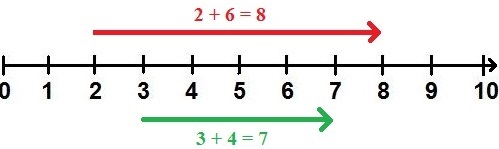
In unserem Beispiel sind die Zahlen 2 und 3 die 1. Summanden. Nach dem Pluszeichen sind 6 und 4 die 2. Summanden. Die Zahlen 8 und 7 sind die Lösungen der Additionen und werden als Summe bezeichnet.

Die Reihenfolge der Zahlen bei einer Addition spielt keine Rolle. Sowohl 2 + 3 als auch 3 + 2 ergeben jeweils 5 als Ergebnis. Die beiden Summanden können vertauscht werden ohne an der Summe eine Änderung zu bewirken. Mehr zum Vertauschen der Zahlen findest du unter Kommutativgesetz.

Anzeigen:

Wie heißen die Teile einer Subtraktion?

Eine Subtraktion erkennst du an einem Minuszeichen (-). Die Zahl vor dem Minuszeichen wird Minuend genannt. Die Zahl nach dem Minuszeichen wird Subtrahend genannt. Das Ergebnis einer Subtraktion ist die Differenz.

Bei der Subtraktion wird etwas "abgezogen". Von einer Zahl wird eine andere Zahl "weggenommen". Die Subtraktion ist damit die Umkehrung der Addition. Sehr einfach zu verstehen ist die Subtraktion an einem Zahlenstrahl. Zwei Beispiele:

• Von der 8 um 6 nach links bringt uns auf die 2.
  • 8 - 6 = 2
• Von der 7 um 4 nach links bringt uns auf die 3.
  • 7 - 4 = 3.

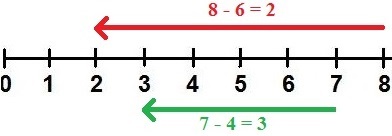
Bei den zwei Beispielen am Zahlenstrahl sind 8 und 7 die Minuenden. Die 6 und die 4 sind die Subtrahenden. Die Differenzen sind die Zahlen 2 und 3.

Im Gegensatz zur Addition ist die Reihenfolge der Zahlen bei einer Subtraktion wichtig. Die Aufgabe 4 - 3 hat ein anderes Ergebnis als die Aufgabe 3 - 4. Minuend und Subtrahend dürfen nicht vertauscht werden! Mehr zum Vertauschen der Zahlen findest du unter Kommutativgesetz.

Wie lauten die Begriffe zur Multiplikation?

Die dritte Grundrechenart wird als Multiplikation bezeichnet. Die Multiplikation ist eine Abkürzung der Addition, denn jede Multiplikation kann durch eine Addition ersetzt werden.

Eine Multiplikation erkennst du an einem Malzeichen (entweder · oder *). Die Zahl vor dem Malzeichen ist der 1. Faktor. Die Zahl nach dem Malzeichen ist der 2. Faktor. Das Ergebnis der Multiplikation wird als Produkt bezeichnet.

Sehen wir uns ein Beispiel zur Multiplikation an: Die Aufgabe 4 + 4 + 4 bedeutet nichts anderes als das wir 3 Mal die Zahl 4 haben.

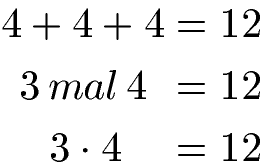
Bei 3 · 4 = 12 ist die 3 der 1. Faktor, die 4 der 2. Faktor und die 12 das Produkt.

Die Reihenfolge der Zahlen bei einer Multiplikation spielt keine Rolle. Sowohl 2 · 3 als auch 3 · 2 ergeben jeweils 6 als Ergebnis. Die beiden Faktoren können vertauscht werden ohne am Produkt eine Änderung zu bewirken. Mehr zum Vertauschen der Zahlen findest du unter Kommutativgesetz.

Wie heißen die Teile einer Division?

Eine Division erkennst du an einem Geteiltzeichen (:). Die Zahl vor dem Geteiltzeichen ist der Dividend. Die Zahl nach dem Geteiltzeichen ist der Divisor. Das Ergebnis der Berechnung wird Quotient genannt.

Dividieren bedeutet nichts anderes als "aufteilen". Die Division ist die Umkehrung der Multiplikation. Zum besseren Verständnis sehen wir uns noch ein Beispiel an und zeigen für dieses Beispiel noch einmal die Fachbegriffe zur Division.

Beispiel: 6 blaue Bälle sollen gleichmäßig auf 2 Körbe aufgeteilt werden. Dies bedeutet 3 Bälle in jeden Korb. Daher ist 6 : 2 = 3.

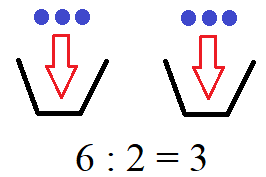
In diesem Beispiel ist die 6 der Dividend, die 2 der Divisor und die 3 der Quotient.

Wie heißen die Fachbegriffe der Grundrechenarten?

Zur besseren Übersicht findest du die Fachbegriffe der Grundrechenarten hier noch einmal kurz zusammengefasst:

• Addition: 1. Summand + 2. Summand = Summe
• Subtraktion: Minuend - Subtrahend = Differenz
• Multiplikation: 1. Faktor · 2. Faktor = Produkt
• Division: Dividend : Divisor = Quotient

Die Fachbegriffe für die Ergebnisse der Grundrechenarten lauten damit:

• Das Ergebnis der Addition ist die Summe.
• Das Ergebnis der Subtraktion ist die Differenz.
• Das Ergebnis der Multiplikation ist das Produkt.
• Das Ergebnis der Division ist der Quotient.

Werden die Zahlen größer tun sich viele Schüler und Schülerinnen sehr schwer diese im Kopf oder auf dem Papier in einem einzelnen Schritt zu berechnen. Aus diesem Grund werden in der Grundschule schriftliche Rechenverfahren eingeführt. Diese findest du unter:

• Schriftliche Addition
• Schriftliche Subtraktion
• Schriftliche Multiplikation
• Schriftliche Division