Schriftliche Addition ▷ Beispiele und Erklärungen

Wie funktioniert die schriftliche Addition ohne Übertrag und mit Übertrag? Wie bekommt man eine Einführung in dieses Thema wie man sie für die Grundschule benötigt? Diese Antworten und mehr bekommst du hier. Ich versuche alles so einfach zu erklären, wie ich dies selbst bei meiner Oma (lange aus der Schule raus) tun würde.

Die schriftliche Addition wird eingesetzt wenn Zahlen etwas größer werden und diese addiert werden sollen. Die Zahlen werden untereinander geschrieben um die Berechnung der Addition zu vereinfachen.

Sehen wir uns nun an, wie man die schriftliche Addition berechnet.

Wie geht die schriftliche Addition? Mit Beispielen!

Bei der schriftlichen Addition werden die Zahlen so untereinander geschrieben, dass die entsprechenden Stellen jeweils untereinander stehen: Einer unter Einer, Zehner unter Zehner und so weiter. Danach wird von hinten nach vorne einzeln addiert.

Beispiel 1 schriftliche Addition ohne Übertrag:

Berechnet werden soll 26 + 51. Wir schreiben die Zahlen so untereinander, dass jeweils die letzte Stelle untereinander steht. Danach rechnen wir von hinten nach vorne und schreiben das Ergebnis unter einen Strich.

• 6 + 1 = 7
• 2 + 5 = 7

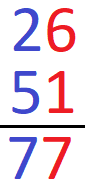
Beispiel 2: Schriftliche Addition ohne Übertrag

Im zweiten Beispiel soll 123 + 412 + 234 berechnet werden. Auch hier schreiben wir die Zahlen untereinander. Dabei stehen die Einer (rot), die Zehner (blau) und die Hunderter (grün) jeweils untereinander. Im Anschluss rechnen wir von hinten nach vorne und schreiben das Ergebnis jeweils unter den Strich:

• 3 + 2 + 4 = 9
• 2 + 1 + 3 = 6
• 1 + 4 + 2 = 7

Anzeigen:

Wie funktioniert die schriftliche Addition mit Übertrag?

Addiert man eine einzelne Stelle und das Ergebnis ist 10 oder größer bekommt man einen Übertrag. Dies bedeutet, dass man auf die Stelle davor eine Zahl mit übernimmt.

Beispiel 3: Schriftliche Addition mit Übertrag:

Berechnet werden soll 53 + 18. Auch hier schreiben wir wieder die Einer (rot) und die Zehner (blau) untereinander. Danach rechnen wir erneut von hinten nach vorne:

• 3 + 8 = 11
• Wir schreiben von der 11 die hintere 1 in das Ergebnis und die vordere 1 nehmen wir mit auf die Zehnerstelle. Dies markieren wir uns mit einer 1 oder einem kleinen Punkt.
• Auf der Zehnerstelle: 5 + 1 = 6. Fehlt uns noch die 1 als Übertrag, daher 6 + 1 = 7.

Wie funktioniert die schriftliche Addition bei mehr als zwei Zahlen?

Wie viele Zahlen addiert werden sollen spielt keine Rolle. Stets werden alle Zahlen mit Einer, Zehner, Hunderter und so weiter untereinander geschrieben. Stelle für Stelle wird von hinten nach vorne addiert. Sehen wir uns zur schriftlichen Addition mit Übertrag ein Beispiel mit Erklärungen an

Beispiel 4: Schriftliche Addition mehrere Zahlen

Nehmen wir einmal ein etwas schwierigeres Beispiel mit 418 + 539 + 669.

• Auch hier schreiben wir die Stellen jeweils untereinander.
• Einerstelle: 8 + 9 + 9 = 26.
  • Daher schreiben wir die 6 in das Ergebnis und die 2 eine Stelle weiter nach vorne. Alternativ können wir wieder Punkte setzen, dies wird jedoch bei mehreren Punkten unübersichtlich.
• Auf der Zehnerstelle 1 + 3 + 6 + 2 = 12.
  • Heißt ich schreibe die 2 hinten in das Ergebnis und die 1 nach vorne.
• Und auf der Hunderterstelle 4 + 5 + 6 + 1 = 16. Die 6 in das Ergebnis und 1 nach vorne. Daher bleibt vorne nur noch eine 1 auf der Tausenderstelle stehen.

Als nächstes empfehle ich noch die schriftliche Addition mit Kommazahlen.

Aufgaben / Übungen schriftlich Addieren

Aufgabe 1: Glaubt ihr das Thema schriftlich Addieren verstanden zu haben? Möchtet ihr das Thema ein bisschen üben? Wir bieten euch hier die Möglichkeit Aufgaben zu rechnen und sich die Lösung dabei anzusehen. Aufgaben können per Klick übersprungen werden.

• Berechne 12 + 36. Wie lautet das Ergebnis?

• 40
• 48
• 52
• 47

Weiter zur Lösung » Aufgabe überspringen »

Du hast 0 von 8 Aufgaben erfolgreich gelöst.