Schriftliche Subtraktion ▷ Beispiele und Erklärung

Wie funktioniert die schriftliche Subtraktion? Was muss man beachten? Wie funktioniert das mit dem Abziehverfahren und dem Ergänzungsverfahren? Diese Antworten und mehr bekommst du hier als Text und als Video. Ich versuche alles so einfach zu erklären, wie ich dies selbst bei meiner Oma (lange aus der Schule raus) tun würde.

Die schriftliche Subtraktion dient dazu größere Zahlen zu subtrahieren. Die Zahlen werden dabei untereinander geschrieben: Einer unter Einer, Zehner unter Zehner und so weiter. Bei der Berechnung gibt es zwei Möglichkeiten: Abziehverfahren und Ergänzungsverfahren. Beide Verfahren mit Beispielen sehen wir uns hier an.

Tipp: In der Regel macht man normalerweise erst die schriftliche Addition und erst danach die schriftliche Subtraktion. Es ist hilfreich, wenn du bereits die schriftliche Addition kennst. Wir sehen uns hier die Grundlagen der schriftlichen Subtraktion an. Im Anschluss könnt ihr euch gerne die Fortsetzung unter schriftliche Subtraktion mit Übertrag und schriftliche Subtraktion mit Komma ansehen.

Wie funktioniert die schriftliche Subtraktion?

Bei der schriftlichen Subtraktion werden die Zahlen untereinander geschrieben. Dabei steht Einer unter Einer (hier rot), Zehner unter Zehner (hier blau), Hunderter unter Hundertern (hier grün) und so weiter.

Das Minuszeichen vor der zweiten Zahl macht klar, dass es hier eine Subtraktion gibt. Das Ergebnis (Differenz) schreiben wir unter den Strich.

Beispiel für eine schriftliche Subtraktion

Wie man eine schriftliche Subtraktion ausrechnest, lernst du weiter unten. Es folgt erst einmal ein Beispiel wie so eine Berechnung am Ende aussehen soll.

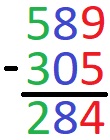
Es gibt zwei Möglichkeiten die schriftliche Subtraktion zu berechnen. Sowohl das Abziehverfahren als auch das Ergänzungsverfahren sehen wir uns in den nächsten Abschnitten mit Beispielen an.

Anzeigen:

Wie funktioniert die schriftliche Subtraktion mit dem Abziehverfahren?

Bei der schriftlichen Subtraktion mit dem Abziehverfahren werden erst einmal die Zahlen untereinander geschrieben. Wir gehen so vor:

• Einer unter Einer, Zehner unter Zehner, Hunderter unter Hunderter und so weiter.
• Ein Minuszeichen vor die zweite Zahl und ein Strich unter die Aufgabe.
• Von hinten nach vorne wird Stelle für Stelle abgezogen (Siehe Beispiel).
• Das Ergebnis wird unter den Strich geschrieben.

Beispiel: Schriftliche Subtraktion mit Abziehverfahren:

Berechnet werden soll 589 - 305. Wir schreiben die Zahlen untereinander. Erst die Berechnung, darunter die Erklärung.

Wir ziehen ab. Dazu nehmen wir die obere Zahl und ziehen von dieser die untere Zahl ab:

• 9 - 5 = 4
• 8 - 0 = 8
• 5 - 3 = 2

Die Berechnung lautet damit: 589 - 305 = 284.

Dieses Beispiel kann auch mit dem Ergänzungsverfahren gerechnet werden. Dies machen wir im nächsten Beispiel.

Wie funktioniert die schriftliche Subtraktion mit dem Ergänzungsverfahren?

Bei der schriftlichen Subtraktion mit dem Ergänzungsverfahren werden die Zahlen werden untereinander geschrieben. Wir gehen so vor:

• Einer unter Einer, Zehner unter Zehner, Hunderter unter Hunderter und so weiter.
• Ein Minuszeichen vor die zweite Zahl und ein Strich unter die Aufgabe.
• Von hinten nach vorne wird Stelle für Stelle ergänzt (Siehe Beispiel).
• Das Ergebnis wird unter den Strich geschrieben.

Beispiel: Schriftliche Subtraktion mit Ergänzungsverfahren:

Berechnet werden soll 589 - 305. Wir schreiben die Zahlen untereinander. Erst die Berechnung, darunter die Erklärung.

Hier geht man bei der Berechnung von der unteren Zahl aus. 5 plus was ergibt 9? Dies macht man für jede Stelle.

• 5 + 4 = 9
• 0 + 8 = 8
• 3 + 2 = 5

Dies waren einfache Beispiele zur schriftlichen Subtraktion. Schwierige Beispiele sehen wir uns unter schriftliche Subtraktion mit Übertrag und schriftliche Subtraktion mit Komma an.

Aufgaben / Übungen schriftlich Subtrahieren

Aufgabe 1: Glaubt ihr das Thema schriftlich Subtrahieren verstanden zu haben? Möchtet ihr das Thema ein bisschen üben? Wir bieten euch hier die Möglichkeit Aufgaben zu rechnen und sich die Lösung dabei anzusehen. Aufgaben können per Klick übersprungen werden. Bevor wir rechnen jedoch erst einmal eine einfache Frage zum Einstieg:

• Wozu verwendet man die schriftliche Subtraktion?

• Große Zahlen multiplizieren
• Große Zahlen dividieren
• Große Zahlen addieren
• Große Zahlen subtrahieren

Weiter zur Lösung » Aufgabe überspringen »

Du hast 0 von 6 Aufgaben erfolgreich gelöst.