Schriftliche Subtraktion mit Übertrag

Wie funktioniert die schriftliche Subtraktion mit Übertrag? Was muss man beachten? Wie funktioniert das mit dem Abziehverfahren und dem Ergänzungsverfahren? Diese Antworten und mehr bekommst du hier als Text und als Video. Ich versuche alles so einfach zu erklären, wie ich dies selbst bei meiner Oma (lange aus der Schule raus) tun würde.

Die schriftliche Subtraktion mit Übertrag dient dazu Subtraktionsaufgaben mit größeren Zahlen zu berechnen. Dabei ist eine Stelle der zweiten Zahl (Subtrahend) größer als bei der ersten Zahl (Minuend). Dies führt zu einem Übertrag. Beispiele und Erklärungen dazu sehen wir uns gleich an.

Die schriftliche Subtraktion mit Übertrag kann mit zwei verschiedenen Verfahren berechnet werden: Dem Abziehverfahren und dem Ergänzungsverfahren. Beide Verfahren sehen wir uns gleich an. Tipp: Es ist hilfreich, wenn du bereits die Grundlagen der schriftlichen Subtraktion ohne Übertrag kennst.

Wie funktioniert die schriftliche Subtraktion beim Abziehverfahren mit Übertrag?

Beim Abziehverfahren der schriftlichen Subtraktion - egal ob ein Übertrag entstehen wird oder nicht - werden die Zahlen Stelle für Stelle untereinander geschrieben: Einer unter Einer, Zehner unter Zehner, Hunderter unter Hunderter und so weiter.

Vor die zweite Zahl wird ein Minuszeichen (-) geschrieben. Von hinten nach vorne wird Stelle für Stelle abgezogen. Ist die Zahl oben kleiner als die Zahl unten erfolgt ein Übertrag. Das nächste Beispiel zeigt das Abziehverfahren.

Beispiel: Abziehverfahren schriftliche Subtraktion mit Übertrag

Berechnet werden soll 567 - 239. Auch hier sind die Einer, Zehner und Hunderter jeweils untereinander geschrieben. Zunächst die Rechnung, darunter die Erklärung:

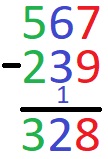
Starten wir mit dem Abziehverfahren. Dieses beginnt bei der oberen Zahl.

• 7 - 9 geht nicht.
  • Daher wandeln wir 1 Zehner in 10 Einer um. Aus 7 wird 17.
  • 17 - 9 = 8.
  • Wir schreiben die 8 ins Ergebnis und notieren uns den Übertrag von 1.
• 6 - 3 = 3 wäre eine falsche Rechnung, dies würde den Übertrag nicht berücksichtigen
  • Wir ziehen die 1 von der 6 ab. Mit 5 - 3 = 2 berücksichtigen wir den Übertrag und erhalten eine 2 für das Ergebnis. Kein Übertrag.
• 5 - 2 = 3. Wir haben eine 3 für unser Ergebnis auf der Hunderterstelle.

Anzeigen:

Wie funktioniert das Ergänzungsverfahren bei der schriftlichen Subtraktion mit Übertrag?

Beim Ergänzungsverfahren der schriftlichen Subtraktion werden die Zahlen Stelle für Stelle untereinander geschrieben: Einer unter Einer, Zehner unter Zehner, Hunderter unter Hunderter und so weiter.

.

Vor die zweite Zahl wird ein Minuszeichen (-) geschrieben. Von hinten nach vorne wird Stelle für Stelle ergänzt. Ist die Zahl oben kleiner als die Zahl unten erfolgt ein Übertrag. Dies siehst du im nächsten Beispiel.

Beispiel: Ergänzungsverfahren schriftliche Subtraktion mit Übertrag

Berechnet werden soll 567 - 239. Zunächst die Rechnung, darunter die Erklärung.

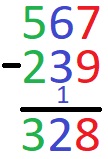
Wie man auf der Einerstelle sehen kann, ist die 7 oben kleiner als die 9, die abgezogen werden sollen. Daher sieht die Rechnung wie folgt aus:

• 9 + ____ = 17.
  • 9 + 8 = 17.
  • Wir schreiben die 8 ins Ergebnis und die 1 als Übertrag.
• 1 + 3 + ___ = 6.
  • 1 + 3 + 2 = 6.
  • Auf dem ___ fehlt uns eine 2, die wir ins Ergebnis übernehmen. Ein Übertrag existiert hier nicht.
• 2 + ___ = 5
  • 2 + 3 = 5
  • Wir schreiben eine 3 in unser Ergebnis.

Als nächstes sehen wir uns die schriftliche Subtraktion mit Komma an.

Aufgaben / Übungen schriftliche Subtraktion

Aufgabe 1: Glaubt ihr das Thema schriftlich Subtrahieren verstanden zu haben? Möchtet ihr das Thema ein bisschen üben? Wir bieten euch hier die Möglichkeit Aufgaben zu rechnen und sich die Lösung dabei anzusehen. Aufgaben können per Klick übersprungen werden. Bevor wir rechnen jedoch erst einmal eine einfache Frage zum Einstieg:

• Wozu verwendet man die schriftliche Subtraktion?

• Große Zahlen addieren
• Große Zahlen multiplizieren
• Große Zahlen subtrahieren
• Große Zahlen dividieren

Weiter zur Lösung » Aufgabe überspringen »

Du hast 0 von 6 Aufgaben erfolgreich gelöst.