Subtrahieren (Mathe) ▷ Beispiele und Erklärungen

Was versteht man unter Subtraktion? Wie subtrahiert man kleine Zahlen? Wie funktioniert die Subtraktion bei großen Zahlen? Wie funktionieren halbschriftliche und schriftliche Subtraktion? Diese Antworten und mehr bekommst du hier als Text und als Video. Ich versuche alles so einfach zu erklären, wie ich dies selbst bei meiner Oma (lange aus der Schule raus) tun würde.

Subtraktion bedeutet nichts anderes als "abziehen" oder "wegnehmen". Ich habe 8 Äpfel und nehme 6 Äpfel weg. Es bleiben 2 Äpfel übrig. Die Subtaktion ist eine der vier Grundrechenart der Mathematik.

Subtraktionen kann man sich sehr einfach am Zahlenstrahl vorstellen. Die nächste Grafik zeigt einen Zahlenstrahl mit zwei kleinen Aufgaben:

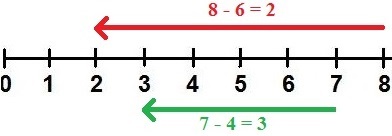
Durch die Subtraktion am Zahlenstrahl lässt sich dies lernen:

• Von der 8 um 6 nach links bringt uns auf die 2.
  • 8 - 6 = 2
• Von der 7 um 4 nach links bringt uns auf die 3.
  • 7 - 4 = 3.

Wie lauten die Fachbegriffe bei der Subtraktion?

Die Zahlen bei der Subtraktion tragen Fachbegriffe. Vor dem Minuszeichen findet sich der Minuend. Die Zahl nach dem Minuszeichen wird als Subtrahend bezeichnet. Das Ergebnis der Berechnung wird Differenz genannt.

Minuend, Subtrahend und Differenz. Diese drei Begriffe zur Subtraktion solltest du dir merken. Sie tauchen im Mathematik-Unterricht immer mal wieder auf.

Im Gegensatz zur Addition ist die Reihenfolge der Zahlen bei einer Subtraktion sehr wichtig. Die Aufgabe 9 - 6 hat ein anderes Ergebnis als die Aufgabe 6 - 9. Minuend und Subtrahend dürfen aus diesem Grund nicht vertauscht werden! Mehr zum Vertauschen der Zahlen findest du unter Kommutativgesetz.

Einfache Aufgaben zur Subtraktion lassen sich im Kopf rechnen oder in einem einzigen Schritt auf dem Papier. Werden die Zahlen größer lässt sich die Aufgabe mit schriftlichen Rechenverfahren besser lösen. Daher sehen wir uns nun noch die halbschriftliche Subtraktion und die schriftliche Subtraktion an.

Anzeigen:

Wie funktioniert die halbschriftliche Subtraktion?

Werden die Zahlen etwas größer hilft einem oftmals bereits die halbschriftliche Subtraktion. In der 2. Klasse oder 3. Klasse wird diese im Zahlenraum bis 100 oder manchmal auch bis 1000 eingesetzt. Bei der halbschriftlichen Subtraktion wird eine Aufgabe in kleinere Teilaufgaben zerlegt. Die Teilaufgaben werden einzeln berechnet.

Beispiel: halbschriftliche Subtraktion

Berechnet werden soll 568 - 482. Um diese auszurechnen, zerlegen wir die 482 in 400, 80 und 2. Diese ziehen wir nach und nach ab. Daher erhalten wir 568 - 482 = 86.

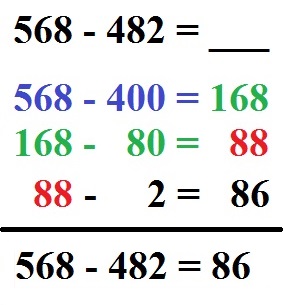
Wichtig bei der halbschriftlichen Subtraktion ist, dass ihr die Einzelrechnungen ohne Fehler durchführen könnt. Ein Fehler bei einer der Rechnungen führt zu einem falschen Gesamtergebnis.

Weitere Erklärungen und Beispiele unter halbschriftliche Subtraktion.

Wie funktioniert die schriftliche Subtraktion?

Für die Subtraktion großer Zahlen wird in der Grundschule die schriftliche Subtraktion verwendet. Bei der schriftlichen Subtraktion werden die Zahlen untereinander geschrieben. Es gibt zwei Möglichkeiten zu rechnen: ergänzen oder abziehen. In beiden Fällen wird von hinten nach vorne Stelle für Stelle vorgegangen.

Beispiel: schriftliche Subtraktion mit Abziehverfahren

Sehen wir uns ein Beispiel mit dem Abziehverfahren an. Berechnet werden soll 586 - 302. Bei der Berechnung werden die einzelnen Stellen untereinander geschrieben. Zuerst die Rechnung, danach die Erklärung:

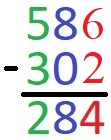
Wir rechnen von hinten nach vorne:

• 6 - 2 = 4
• 8 - 0 = 8
• 5 - 3 = 2

Wichtig: Bei der schriftlichen Subtraktion müssen Einer unter Einer (hier rot), Zehner und Zehner (hier blau) und so weiter stehen.

Dies war ein sehr einfaches Beispiel mit dem Abziehverfahren. Es war vor allem deshalb einfach, da hier kein Übertrag stattgefunden hat. Wie man schwierigere Aufgaben - auch mit Übertrag - löst, findest du zusammen mit weiteren Erklärungen, Beispielen und auch dem Ergänzungsverfahren unter schriftliche Subtraktion.

Aufgaben (Übungen) Subtraktion

Aufgabe 1: Glaubt ihr das Thema schriftlich Subtrahieren verstanden zu haben? Möchtet ihr das Thema ein bisschen üben? Wir bieten euch hier die Möglichkeit Aufgaben zu rechnen und sich die Lösung dabei anzusehen. Aufgaben können per Klick übersprungen werden. Bevor wir rechnen jedoch erst einmal eine einfache Frage zum Einstieg:

• Wozu verwendet man die schriftliche Subtraktion?

• Große Zahlen addieren
• Große Zahlen multiplizieren
• Große Zahlen subtrahieren
• Große Zahlen dividieren

Weiter zur Lösung » Aufgabe überspringen »

Du hast 0 von 6 Aufgaben erfolgreich gelöst.