Multiplizieren (Mathe) ▷ Beispiele und Erklärungen

Was ist multiplizieren? Wie multipliziert man kleine und große Zahlen? Welche Begriffe sind bei der Multiplikation wichtig? Wie funktionieren halbschriftliche und schriftliche Multiplikation? Diese Antworten und mehr bekommst du hier als Text und als Video. Ich versuche alles so einfach zu erklären, wie ich dies selbst bei meiner Oma (lange aus der Schule raus) tun würde.

Die Multiplikation ist eine Abkürzung für eine Addition. Neben Addition, Subtraktion und Division ist die Multiplikation eine der vier Grundrechenarten. Das Zeichen für die Multiplikation ist das Malzeichen. Meistens dargestellt mit · oder *.

Wie multipliziere ich kleine Zahlen?

Kleine Multiplikationsaufgaben bis 10 · 10 = 100 nennt man das Einmaleins. Wenn du gerade erst mit dem Multiplizieren startest, solltest du mit dem Einmaleins beginnen und die Multiplikation mit Hilfe einer Addition lösen.

Beispiel 1: Multiplizieren

Die Additionsaufgabe 4 + 4 + 4 bedeutet nichts anderes als das wir 3 Mal die Zahl 4 haben. Wir können dies umwandeln in eine Aufgabe zur Multiplikation. Sowohl die Addition 4 + 4 + 4 ergibt 12 als auch die Multiplikation mit 3 · 4 gleich 12.

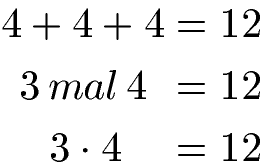
Beispiel 2 Multiplikation:

Sehen wir uns ein weiteres, einfaches Beispiel zur Multiplikation an. Die Additionsaufgabe 8 + 8 + 8 bedeutet nichts anderes als das wir 3 Mal die Zahl 8 haben. In beiden Fällen ist das Ergebnis 24.

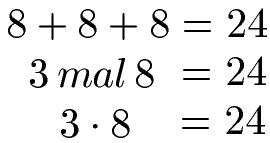
Beispiel 3 Multiplikation:

Aller guten Dinge sind drei. So lautet zumindest ein Sprichwort. Daher noch ein drittes Beispiel: Die Additionsaufgabe 5 + 5 + 5 + 5 bedeutet nichts anderes als das wir 4 Mal die Zahl 5 haben. Auch hier erhalten wir als Ergebnis 20.

Anzeigen:

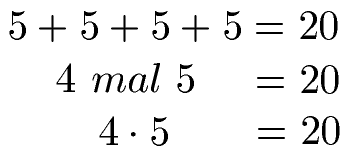
Wie heißen die Teile der Multiplikation?

Bei der Multiplikation unterscheidet man zwischen Faktoren und Produkt. Vor der Malzeichen steht der 1. Faktor. Nach dem Malzeichen findest du den 2. Faktor. Das Ergebnis der Berechnung wird als Produkt bezeichnet.

In manchen Mathematik-Büchern oder auf manchen Websites wird nicht nach 1. Faktor und 2. Faktor unterschieden. Diese werden manchmal einfach nur Faktoren genannt. Daran sollte man sich jedoch nicht groß stören.

Die Reihenfolge der Zahlen beim Multiplizieren spielt keine Rolle. Sowohl 5 · 4 als auch 4 · 5 ergeben jeweils 20 als Produkt. Die beiden Faktoren können damit beliebig vertauscht werden ohne das Ergebnis der Berechnung zu verändern. Mehr dazu findest du unter Kommutativgesetz. Die Multiplikation ist eine Grundrechenart der Mathematik.

Was bedeutet multiplizieren?

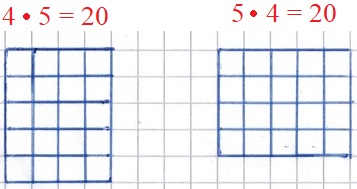
Eine Multiplikation ist nichts anderes als eine Abkürzung für eine Addition. Dies kann man sehr einfach an einem Beispiel mit Kästchen sehen. Ich kann jeweils 4 Kästchen in 5 Zeilen haben oder 5 Kästchen in 4 Zeilen. In beiden Fällen komme ich auf 20 Kästchen.

Alternativ kann dies auch per Addition gerechnet werden:

• 5 + 5 + 5 + 5 = 20
• 4 + 4 + 4 + 4 + 4 = 20

Wie man hier klar sehen kann ist die Schreibweise in Form einer Multiplikation kürzer und einfacher. Möchtest du eine Multiplikation umkehren kannst du dies mit einer Division tun.

Unter dem kleinen Einmaleins versteht man Multiplikationsaufgaben von 1 · 1 = 1 bis 10 · 10 = 100. Es ist - auch für später in der Schule - sehr hilfreich, wenn du das Einmaleins auswendig lernst. Ich weiß, dass auswendig lernen extrem unbeliebt ist. Es macht dennoch Sinn kleinere Multiplikationen im Kopf zu haben.

Für die Multiplikation größerer Zahlen sehen wir uns in den nächsten Abschnitten die halbschriftliche Multiplikation und die schriftliche Multiplikation an.

Was ist die halbschriftliche Multiplikation?

Die halbschriftliche Multiplikation dient dazu etwas größere Zahlen zu multiplizieren. Dabei wird eine Zahl in Einer, Zehner, Hunderter usw. zerlegt und einzeln multipliziert. Die Teilergebnisse werden addiert.

Beispiel: Multiplikation halbschriftlich

Berechnet werden soll 5 · 125. Die 125 zerlegen wir in 100, 20 und 5 und multiplizieren diese einzeln mit der 5. Die Ergebnisse rechnen wir zusammen und erhalten 625 als Produkt.

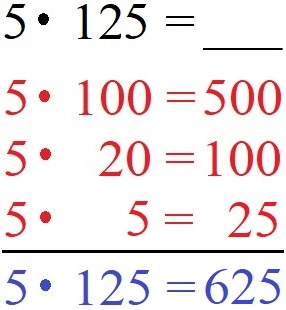
Der erste Faktor - also die 5 vorne - besteht dabei nur aus einer Stelle. Hätten wir hier eine deutlich größere Zahl würde dies die Rechnung viel schwieriger machen. Aus diesem Grund sehen wir uns im nächsten Abschnitt die schriftliche Multiplikation an.

Wie funktioniert die schriftliche Multiplikation?

Die schriftliche Multiplikation dient dazu größere Zahlen zu multiplizieren. Sie funktioniert sowohl für einstellige Zahlen als auch für mehrstellige Zahlen. Bei der schriftlichen Multiplikation wird die Aufgabe in mehrere kleine Multiplikationen zerlegt.

Beispiel 1: Multiplikation schriftlich ohne Übertrag

Wie lautet die Lösung der Aufgabe 2341 · 2? Lösung:

Wir multiplizieren die 2 hinten mit jeder Ziffer der ersten Zahl:

• 2 · 1 = 2
• 2 · 4 = 8
• 2 · 3 = 6
• 2 · 2 = 4

Beispiel 2: Multiplikation schriftlich mit Übertrag

Berechnet werden soll 2341 · 4. Auch hier zerlegen wir in kleinere Multiplikationen. Bei diesen entsteht jedoch manchmal eine Zahl die größer als 9 ist. In diesem Fall muss ein Übertrag auf die nächste Stelle gemacht werden. Zunächst die gelöste Aufgabe, darunter die Erklärung:

Berechnung:

• 4 · 1 = 4. Wir schreiben die 4.
• 4 · 4 = 16. Wir schreiben die 6. Die 1 vorne merken wir uns als Übertrag.
• 4 · 3 = 12. Mit Übertrag erhalten wir 12 + 1 = 13. Die 3 in das Ergebnis und die 1 als Übertrag auf die nächste Stelle.
• 4 · 2 = 8. Mit dem Übertrag der letzten Rechnung 8 + 1 = 9. Die 9 kommt in unser Ergebnis.

Beispiel 3: Multiplikation schriftlich mit zweistelliger Zahl

Sehen wir uns ein Beispiel mit einer zweistelligen Zahl an. Die Aufgabe lautet 2341 · 12. Auch hier zerlegen wir in kleinere Multiplikationen. Dabei multiplizieren wir zunächst 2341 mit der 1 von der 12 und danach mit der 2 von der 12. Erst die Berechnung, darunter die Erklärung:

Berechnung:

• Starten wir mit der Zehnerstelle der 12, also der 1:
  • 1 · 1 = 1
  • 1 · 4 = 4
  • 1 · 3 = 3
  • 1 · 2 = 2
• Nun die Einerstelle der 12, also die 2:
  • 2 · 1 = 2
  • 2 · 4 = 8
  • 2 · 3 = 6
  • 2 · 2 = 4
  • Beachte: Schreibe die 4682 so, dass diese unter der 2 oben steht.
• Wir müssen jetzt wie bei der schriftlichen Addition einfach die Zahlen zusammenzählen:
  • Die 2 bleibt einfach.
  • 1 + 8 = 9
  • 4 + 6 = 10. Die 0 ins das Ergebnis und den Übertrag von 1 merken.
  • 3 + 4 = 7. Auf die 7 noch 1 vom Übertrag drauf rechnen ergibt 8.
  • Vorne fehlt noch die 2.

Aufgaben / Übungen zur Multiplikation

Aufgabe 1:

Hinweis: Wenn ihr gleich mit der schriftlichen Multiplikation mit Komma starten wollt, dann klickt hier.

Glaubt ihr das Thema schriftlich Multiplizieren (mit und ohne Komma) verstanden zu haben? Möchtet ihr das Thema ein bisschen üben? Wir bieten euch hier die Möglichkeit Aufgaben zu rechnen und sich die Lösung dabei anzusehen. Fragen und Aufgaben können per Klick übersprungen werden. Wie lautet die Lösung dieser Aufgabe?

• 2134 · 2 = ?

• 2143
• 2418
• 4268
• 4247

Weiter zur Lösung » Aufgabe überspringen »

Du hast 0 von 5 Aufgaben erfolgreich gelöst.