Dividieren (Mathematik) ▷ Beispiele und Erklärungen

Was ist dividieren (teilen) eigentlich? Wie dividiert man Zahlen und was ist die Umkehrung der Division? Und wie dividiert man größere Zahlen mit der halbschriftlichen Division oder schriftlichen Division? Diese Antworten und mehr bekommst du hier als Text und als Video. Ich versuche alles so einfach zu erklären, wie ich dies selbst bei meiner Oma (lange aus der Schule raus) tun würde.

Dividieren bedeutet im Deutschen "teilen" oder "aufteilen". Das Zeichen für das Dividieren ist der Doppelpunkt (:) oder manchmal auch der Schrägstrich (/). An einem sehr einfachen Beispiel kann man sich die Division von Zahlen vorstellen: 6 blaue Bälle werden auf 2 Körbe verteilt. Dies bedeutet 3 Bälle pro Korb. Gesprochen: 6 durch 2 gleich 3.

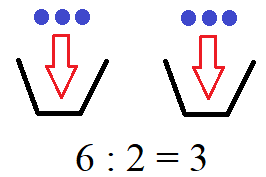
Das Gegenteil von dividieren ist multiplizieren. Dies sehen wir uns weiter unten mit Beispielen an. Sowohl die Division als auch die Multiplikation gehören zu den Grundrechenarten der Mathematik.

Wie heißen die Fachbegriffe der Division?

Im nächsten Abschnitt sehen wir uns gleich an, wie man Zahlen dividiert. Dabei tauchen jedoch immer mal wieder Fachbegriffe zur Division auf. Die verschiedenen Zahlen haben bestimmte Begriffe, die du kennen solltest.

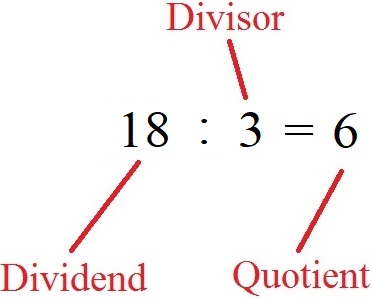
Die erste Zahl vorne wird als Dividend bezeichnet. Nach dem Geteiltzeichen folgt der Divisor. Das Ergebnis der Berechnung wird als Quotient bezeichnet.

Die Reihenfolge der Zahlen beim Dividieren ist wichtig! Die Aufgabe 18 : 3 liefert ein anderes Ergebnis als 3 : 18. Dividend und Divisor dürfen daher nicht vertauscht werden. Mehr dazu findest du unter Kommutativgesetz. Die Division ist eine Grundrechenart der Mathematik.

Anzeigen:

Wie dividiert man Zahlen?

Die Division ist die Umkehrung der Multiplikation. Wer noch nicht multiplizieren kann, wirft bitte erst einmal einen Blick in den Artikel oder das Video unter Multiplikation. Die Divisionen in den nächsten Beispielen verdeutlichen wir uns über die Multiplikation.

Beispiele:

• 24 : 4 = 6, denn
• 6 · 4 = 24

• 12 : 3 = 4, denn
• 4 · 3 = 12

• 30 : 6 = 5, denn
• 5 · 6 = 30

Wer sich bei den kleinen Division nicht ganz sicher ist, der kann sich dies mit Körben und Bällen verdeutlichen. Dies musst du natürlich nicht mit echten Körben und Bällen machen, sondern kannst auch auf dem Papier alles aufzeichnen.

Insbesondere wenn die Zahlen größer werden fällt es vielen Menschen schwer Divisionen im Kopf zu berechnen oder mit einem einzelnen Schritt auf dem Papier. Daher sehen wir uns jetzt noch die halbschriftliche Division und die schriftliche Division an.

Was ist die halbschriftliche Division?

Für etwas größere Zahlen wird die halbschriftliche Division eingesetzt. Dabei wird die Divisionsaufgabe in kleinere Aufgaben zerlegt. Der Dividend wird dabei in kleinere Zahlen zerlegt um einzeln rechnen zu können.

Beispiel Division halbschriftlich:

Berechnet werden soll 384 : 6. Wie lautet das Ergebnis? Dazu zerlegen wir die 384 in Zahlen, welche wir einfach durch 6 teilen können. In diesem Fall habe ich mich für 300, 60 und 24 entschieden. Diese drei Zahlen können einfach durch 6 geteilt werden. Die Ergebnisse 50, 10 und 4 rechnen wir zusammen und erhalten 64 als Ergebnis. Daher ist 384 : 6 = 64.

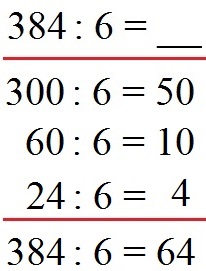
Die halbschriftliche Division lässt sich im Zahlenraum bis 1000 recht gut einsetzen. Werden die Zahlen noch größer wird es hingegen mit dieser Berechnungsart schwierig. Daher sehen wir uns jetzt noch die schriftliche Division an.

Wie funktioniert die schriftliche Division?

Die schriftliche Division wird für das Teilen großer Zahlen eingesetzt. Sie wird meistens ab der 3. Klasse behandelt. Ab der 4. Klasse wird das schriftliche Dividieren mit größeren Zahlen durchgeführt. Außerdem steht die schriftliche Division mit Dezimalzahlen (Kommazahlen) während der Schulzeit ebenfalls auf dem Lehrplan.

Beispiel schriftliche Division:

Berechnet werden soll 735 :3. Wie lautet das Ergebnis?

Lösung:

Wir nehmen die vorderste Ziffer des Dividenden (735), also die 7. Wie oft geht die 3 in die 7 rein? Dies geht 2 Mal. Daher schreiben wir die 2 in unser Ergebnis.

Im nächsten Schritt müssen wir multiplizieren. Dazu nehmen wir die 2 aus dem Ergebnis und multiplizieren diese mit dem Divisor (3). Wir erhalten 2 · 3 = 6. Diese 6 schreiben wir vorne unter die 7.

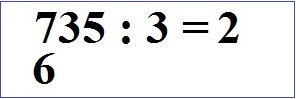
Der nächste Schritt ist eine Subtraktion: 7 - 6 = 1.

Wir ziehen die nächste Stelle vom Dividenden nach unten. In diesem Fall eine 3. Aus der 1 wird dadurch eine 13.

Wie oft geht die 3 (Dividend) in die 13? Dies geht 4 mal. Daher schreiben wir die 4 in unser Ergebnis.

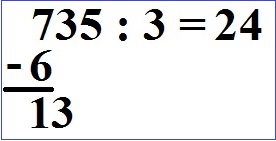
Wir multiplizieren zurück: Die 4 aus dem Ergebnis mal 3 (Divisor) ergibt 12. Die 12 schreiben wir unter die 13.

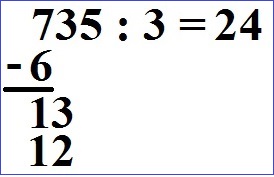
Wir subtrahieren 13 - 12 = 1.

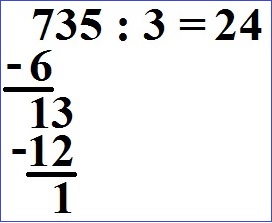
Wir ziehen die nächste Stelle nach unten. Daher wird aus der 1 eine 15.

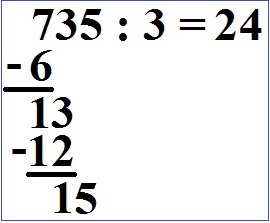
Wir rechnen 15 : 3 = 5. Die 5 kommt in unser Ergebnis.

Wir multiplizieren wieder in die andere Richtung: 5 · 3 = 15.

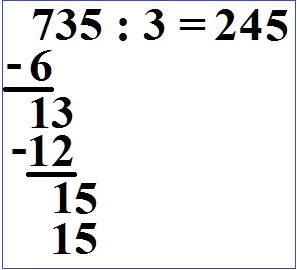
Wir subtrahieren erneut: 15 - 15 = 0.

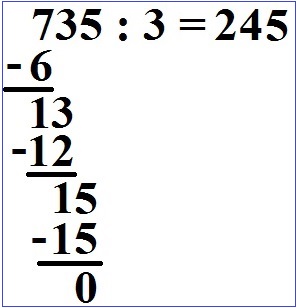
Damit ist die Rechnung komplett. 735 : 3 = 245.