Potenzgesetze Übersicht + Beispiele

Die Potenzgesetze zusammen mit Beispielen bekommst du hier. Zunächst erkläre ich kurz was eine Potenz überhaupt ist und welche Begriffe du kennst solltest. Danach bekommst du eine Übersicht der Potenzgesetze mit Beispielen nach Basis und Exponent unterteilt. Ich versuche die Inhalte so einfach zu erklären, wie ich dies selbst bei meiner Oma (lange aus der Schule raus) tun würde.

Eine Potenz ist in der Mathematik eine Abkürzung für die Multiplikation gleicher Zahlen.

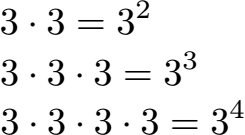
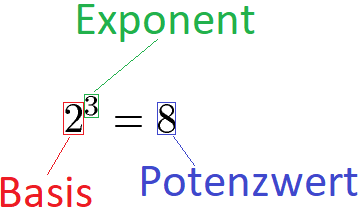
Eine Potenz besteht aus einer Basis und einem Exponenten. Der Exponent ist die kleine Zahl, welche rechts oberhalb der Basis steht. Der Exponent gibt an, wie oft die Basis mit sich selbst multipliziert werden muss. Wird die Potenz ausgerechnet, nennt man das Ergebnis Potenzwert.

Wie lauten die Potenzgesetze bei gleicher Basis?

Bei gleicher Basis und gleichem Exponenten können Potenzen sehr einfach addiert werden. Dazu werden die Koeffizienten (hier a und b) vor der Basis in einer Klammer addiert. Die restliche Basis und der Exponent werden übernommen. Sehen wir uns das Potenzgesetz der Addition mit Beispiel an.

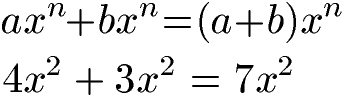
Die Subtraktion bei gleicher Basis (und gleichem Exponenten) funktioniert ebenso wie die Addition. Die nächste Grafik zeigt das Potenzgesetz für die Subtraktion mit Beispiel.

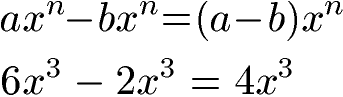
Zwei Potenzgesetze sind für die Multiplikation von Potenzen mit gleicher Basis zu erklären. Bei zwei Potenzen mit gleicher Basis aber unterschiedlichem Exponenten wird die Basis übernommen und die Exponenten werden addiert.

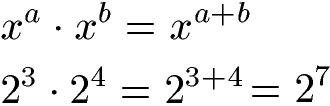
Ein Spezialfall liegt vor bei gleicher Basis und gleichem Exponenten. Hier sieht die Potenzregel vor die Basis in einer Klammer mit sich selbst zu multiplizieren und den Exponenten zu übernehmen.

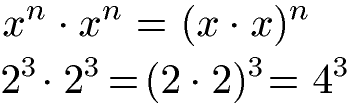
Zwei Potenzgesetze betreffen die Division von Potenzen mit gleicher Basis. Im ersten Fall wird die Basis übernommen während die Exponenten subtrahiert werden.

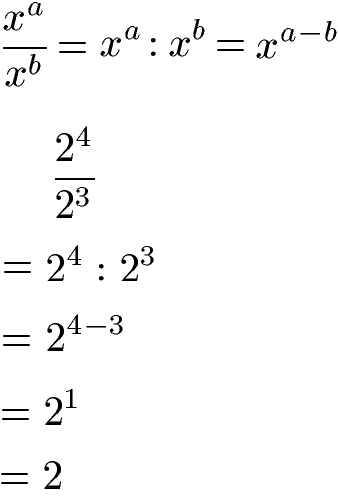
Das Potenzgesetz zur Division bei gleicher Basis und gleichem Exponenten ist besonders einfach: Der Quotient ist stets 1.

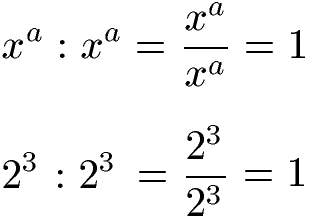
Anzeigen:

Wie lauten die Potenzgesetze für gleiche Exponenten?

Potenzen können bei gleichen Exponenten addiert werden, indem die Koeffizienten addiert werden. Als weitere Voraussetzung müssen jedoch auch die Basen gleich sein. Die Addition der Koeffizienten findet in einer Klammer statt.

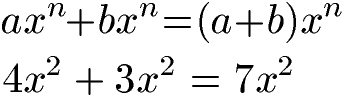
Die Potenzgesetze sagen außerdem, das das Subtrahieren von Potenzen bei gleichen Exponenten ebenfalls möglich ist. Dazu werden die Koeffizienten subtrahiert während Basis und Exponent erhalten bleiben. Auch hier sind jedoch zusätzlich gleiche Basen notwendig.

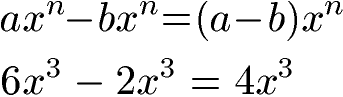
Zwei Potenzregeln für die Multiplikation von Potenzen mit gleichem Exponenten solltest du kennen: Zunächst die Multiplikation von Potenzen mit gleichen Exponenten aber unterschiedlicher Basis. Dabei werden die Basen miteinander in einer Klammer multipliziert, die Hochzahl bleibt erhalten.

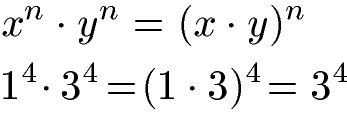
Potenzen können auch bei gleichem Exponenten und gleicher Basis multipliziert werden. Dabei wird in einer Klammer die Basis mit sich selbst multipliziert, der Exponent wird übernommen.

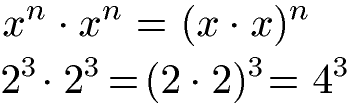
Die Potenzregeln für die Division beginnen beim Dividieren von Potenzen mit gleichem Exponenten, aber unterschiedlichen Basen. Die Division kann dabei sowohl in der Form mit einem Geteiltzeichen vorliegen oder auch als Bruch.

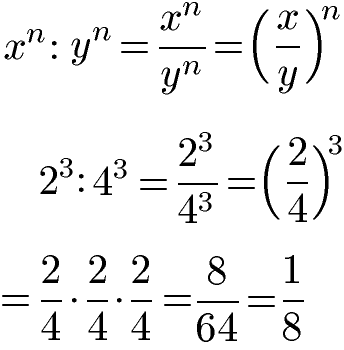
Das Potenzgesetz zur Division bei gleichem Exponenten und gleicher Basis ist besonders einfach: Der Quotient ist stets 1.

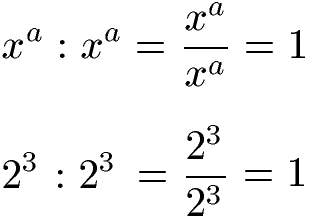
Wie funktionieren die Potenzgesetze für Wurzeln?

Zwei Potenzgesetze dienen dazu Potenzen in Wurzeln umzurechnen oder umgekehrt Wurzeln in Potenzen. Dabei wird die n-te Wurzel aus einer Zahl a zu einer Potenz mit der Basis a und 1 geteilt durch n im Exponenten. Oder umgekehrt: Eine Potenz mit Basis a und 1 : n im Exponenten wird zur n-ten Wurzel aus a.

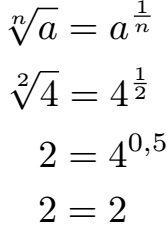
Das eben genannte Potenzgesetz zu Wurzeln kann noch etwas allgemeiner formuliert werden. Dabei wird die n-te Wurzel aus der Potenz a^m zu einer Potenz mit der Basis a und m : n im Exponenten.

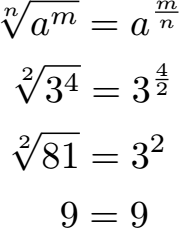
Wie funktionieren Potenzregeln und Klammern zusammen?

Ein häufiger Fehler bei Potenzen besteht im Setzen oder im nicht Setzen von Klammern rund um die Basis. Im nächsten Beispiel ist -6b die Basis. Diese -6b stehen in einer Klammer und werden dabei 3 Mal mit sich selbst multipliziert.

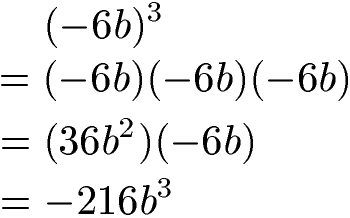
Würden die -6b nicht in Klammern stehen wäre die Basis nur b. Wir würden damit b³ = b · b · b berechnen und dies im Anschluss mit -6 multiplizieren. Die Ergebnisse wären damit völlig verschieden.

Wie potenziert man Potenzen?

Eine Potenz kann potenziert werden, indem die beiden Exponenten miteinander multipliziert werden. Das Produkt der beiden Exponenten stellt dabei den Exponenten einer neuen Potenz da.

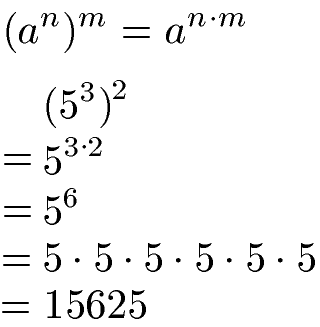
Welches Potenzgesetz gilt für negative Exponenten?

Negative Exponenten können mit einem Bruch in positive Exponenten umgewandelt werden. Dazu wird die ursprüngliche Potenz mit der negativen Zahl im Exponenten in den Nenner eines Bruchs geschrieben und dabei das Vorzeichen vertauscht. Im Zähler des Bruchs steht dabei die Zahl 1.

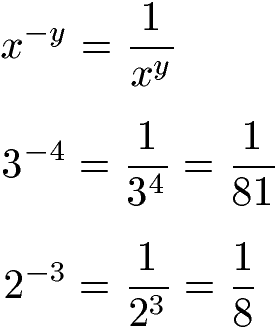
Aufgaben / Übungen Potenzgesetze

Aufgabe 1:

Glaubt ihr das Thema Potenzgesetze verstanden zu haben? Möchtet ihr das Thema ein bisschen üben? Wir bieten euch hier die Möglichkeit Aufgaben zu rechnen und sich die Lösung dabei anzusehen. Fragen und Aufgaben können per Klick übersprungen werden. Wie lautet die Lösung dieser Aufgabe? Verwende die passende Potenzegel.

• 128
• 256
• 32
• 64

Weiter zur Lösung » Aufgabe überspringen »

Du hast 0 von 5 Aufgaben erfolgreich gelöst.