Quadratische Funktion lösen

Kann man das Lösen quadratischer Funktionen bzw. quadratischer Gleichungen so einfach erklären, dass jeder dies versteht? Wir versuchen es hier. Stellt euch vor ein Schüler kommt nach der Schule zu seiner Oma und versucht ihr zu erklären, wie man eine quadratische Funktion / Gleichung berechnet. Glaubt ihr eine echte Oma würde die folgenden Erklärungen verstehen?

Schüler: Wir haben heute in der Schule quadratische Gleichungen gelöst. Weißt du noch wie das geht?

Oma. Nein. Offen gestanden weiß ich nicht mal was eine quadratische Gleichung ist.

Schüler: Bei einer einfachen Gleichung gibt es nur ein x, zum Beispiel 2 + x = 3. Bei einer quadratischen Funktion kommt ein x² vor.

Oma: Mach mal ein Beispiel.

Schüler: Nehmen wir diese Gleichung:

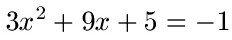
Oma: Und was mache ich mit so einer Gleichung?

Schüler: Einfach gesagt berechnen wir x. Das Problem ist wie man so eine quadratische Gleichung nach x auflöst. Dazu kann ich dir gleich einmal die PQ-Formel und die Mitternachtsformel / ABC-Formel zeigen.

PQ-Formel für quadratische Funktion

Schüler: Die erste Möglichkeit so eine quadratische Gleichung zu lösen ist die PQ-Formel. Um diese benutzen zu können, müssen wir die Gleichung so umformen, dass wir = 0 haben. In diesem Fall rechnen wir +1 auf beiden Seiten der Gleichung

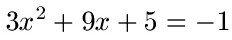
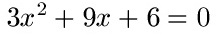
Schüler: Vor dem x² steht eine 3. Die muss weg, es darf nur x² stehen bleiben. Daher teilen wir alles in der Gleichung durch 3.

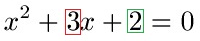
Oma: Wieso hast du die 3 und die 2 farbig markiert?

Schüler: Das ist unser p und unser q. Daher auch der Name PQ-Formel.

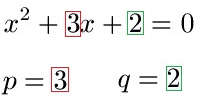
Schüler: Jetzt brauchen wir die Lösungsformel für die PQ-Formel. Das ist diese hier:

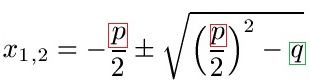
Oma: Sieht kompliziert aus. Was mache ich damit?

Anzeigen:

PQ-Formel: p und q einsetzen

Schüler: Wir setzen in die Lösungsformel der PQ-Formel unser p und q ein.

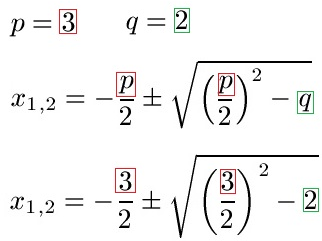
Oma: Jetzt rechnen wir?

Schüler: Ja. Vor der der Wurzel wird aus dem Bruch -3 : 2 einfach -1,5. Unter der Wurzel haben wir diesen Bruch auch noch, müssen ihn jedoch noch quadrieren. Daraus wird 2,25.

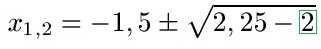
Schüler: Wir rechnen 2,25 - 2 = 0,25 aus. Die Wurzel aus 0,25 ist 0,5.

Oma: Was ist das mit plus und minus vor der Wurzel?

Schüler: Wir haben zwei Ergebnisse. Wir berechnen eine Lösung mit "plus" und eine Lösung mit "-".

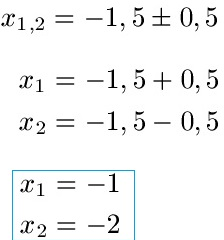
Oma: Die Lösung der quadratischen Funktion ist also x₁ = -1 und x₂ = -2?

Schüler: Ja, genau.

ABC-Formel für quadratische Funktion

Oma: Was ist jetzt mit der Mitternachtsformel?

Schüler: Wer die PQ-Formel nicht mag kann alternativ die Mitternachtsformel (ABC-Formel) verwenden. Nehmen wir noch einmal die quadratische Gleichung:

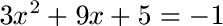
Oma: Vorhin hatten wir als erstes + 1 gerechnet um die -1 rechts zu beseitigen. Machen wir das wieder?

Schüler: Ja. Das machen wir auch. So erhalten wir wieder = 0. Danach können wir sofort a, b und c für die Mitternachtsformel ablesen. Wir müssen im Gegensatz zur PQ-Formel nicht durch 3 teilen, sondern können direkt ablesen.

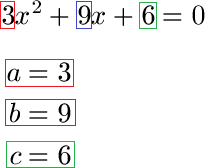
Oma: Gibt es jetzt wieder eine Formel zum Einsetzen?

Schüler: Ja, die ABC-Formel lautet jetzt so:

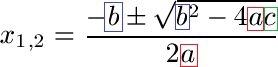
Oma: Was muss ich jetzt tun?

Mitternachtsformel verwenden

Schüler: Wir setzen hier für a, b und c die entsprechenden Zahlen ein, die wir bereits abgelesen haben.

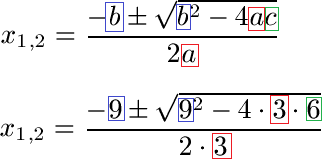
Oma: Wir setzen a = 3, b = 9 und c = 6.

Schüler: Ja. Das rechnen wir aus. Unter der Wurzel erst die Potenz mit 9 · 9 = 81 berechnen. Davon ziehen wir 4 · 3 · 6 = 72 ab und erhalten 9 unter der Wurzel.

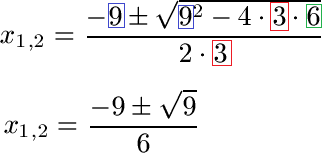
Oma: Da ist wieder plus und minus übereinander. Warum?

Schüler: Das plus-minus bedeutet, dass wir zwei Lösungen für x haben. Wir berechnen den Bruch einmal mit einem plus und einmal mit einem minus. Dadurch erhalten wir wieder zwei Lösungen für die quadratische Gleichung.

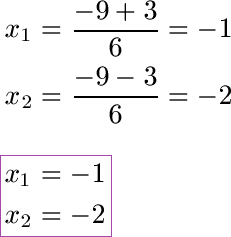
Oma: Das war es?

Schüler: Das war es. Vielleicht sollte man das Ganze noch etwas üben:

• Aufgaben / Übungen PQ-Formel
• Aufgaben / Übungen Mitternachtsformel