Schriftlich multiplizieren mit Kommastellen

Wie funktioniert die schriftliche Multiplikation mit Dezimalzahlen (Kommazahlen)? Wie gehe ich mit einer Stelle oder mehreren Stellen nach dem Komma um? Welche Fehler darf ich nicht machen? Diese Antworten und mehr bekommst du hier als Text und als Video. Ich versuche alles so einfach zu erklären, wie ich dies selbst bei meiner Oma (lange aus der Schule raus) tun würde.

Die schriftliche Multiplikation mit Komma dient dazu Zahlen miteinander zu multiplizieren, bei denen mindestens eine der beiden Zahlen ein Komma aufweist. Das schriftliche Malnehmen ist auch dann hilfreich, wenn die Zahlen relativ klein sind, denn es hilft die Lösung einfach auszurechnen und das Komma im Ergebnis an der richtigen Stelle zu platzieren.

Bei der schriftlichen Multiplikation mit Komma multiplizierst du die beiden Zahlen erst einmal so als würde es kein Komma geben. So wie man dies von der schriftlichen Multiplikation kennt. Zählt bei den beiden Ausgangszahlen (Faktoren) wie viele Stellen sich hinter dem Komma befinden. So viele Stellen wie es bei den Ausgangszahlen hinter dem Komma gibt, so viele Stellen gibt es auch beim Ergebnis (Produkt) hinter dem Komma.

Wie funktioniert das Multiplizieren mit Kommazahlen?

Beim Multiplizieren mit Komma wird schriftlich multipliziert als gäbe es kein Komma. Im Ergebnis muss das Komma so gesetzt werden, dass es der Anzahl der Stellen nach dem Komma bei den Ausgangszahlen entspricht. Sehen wir uns dazu ein Beispiel an.

Beispiel:

Berechnet werden soll 12 · 2,3. Ich zeige dir zunächst die Berechnung und im Anschluss wie alles ausgerechnet wurde.

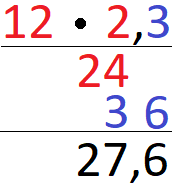
Lösung:

• Zunächst tun wir so, als gäbe es kein Komma.
• In rot haben wir die Multiplikation : 12 · 2 = 24 sowie 12 · 3 = 36.
• Danach addieren wir: Ganz hinten nur eine 6. Davor 4 + 3 = 7 und ganz vorne eine 2.
• Wir zählen bei den beiden Faktoren (Ausgangszahlen) die Stellen nach dem Komma:
  • Bei der 12 gibt es keine Stelle hinter dem Komma.
  • Bei der 2,3 gibt es eine Stelle hinter dem Komma.
  • 0 Stellen + 1 Stelle = 1 Stelle.
  • Damit gibt es im Ergebnis eine Stelle hinter dem Komma. Das Komma sitzt somit vor der 6.

Im nächsten Abschnitt sehen wir uns die schriftliche Multiplikation mit Dezimalzahlen an wenn beide Faktoren ein Komma aufweisen.

Anzeigen:

Wie funktioniert die Multiplikation mit Dezimalzahlen wenn beide Faktoren eine Dezimalzahl sind?

Multipliziere auch in diesem Fall beide Zahlen als würde es kein Komma geben. Zähle bei der ersten Zahl die Stelle(n) hinter dem Komma. Zähle bei der zweiten Zahl die Stelle(n) hinter dem Komma. Addiere diese beiden Informationen. So viele Stellen gibt es nach dem Komma beim Produkt (Ergebnis einer Multiplikation.).

Beispiel: Dezimalzahlen multiplizieren

Multipliziere die Dezimalzahlen 1,2 · 3,21. Wie lautet das Ergebnis? Auch hier erst einmal die Berechnung und unterhalb der Lösungsweg:

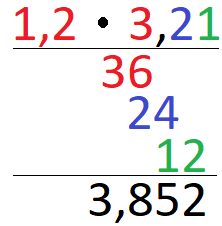
So wurde gerechnet:

• 12 · 3 = 36
• 12 · 2 = 24
• 12 · 1 = 12
• Wir addieren schriftlich: Hinten nur die 2, davor 4 + 1 = 5, davor 6 + 2 = 8 und ganz vorne nur eine 3.
• Bei 1,2 haben wir eine Stelle hinter dem Komma.
• Bei 3,21 haben wir zwei Stellen hinter dem Komma.
• Eine Stelle hinter dem Komma plus zwei Stellen hinter dem Komma macht drei Stellen hinter dem Komma.
• Dadurch wird aus 3852 nun 3,852. Wir haben 3 Stellen hinter dem Komma beim Produkt.

Welche Fehler darf ich beim schriftlichen Multiplizieren mit Komma nicht machen? Du musst bei jeder Zahl immer alle Stellen nach dem Komma Zählen, selbst wenn eine 0 geschrieben wird. Die Anzahl der Stellen nach dem Komma bei den Ausgangszahlen entspricht der Anzahl der Stellen nach dem Komma im Ergebnis der Aufgabe.

Aufgaben / Übungen schriftliche Multiplikation mit Komma

Aufgabe 1:

Hinweis: Wenn ihr gleich mit der schriftlichen Multiplikation mit Komma starten wollt, dann klickt hier.

Glaubt ihr das Thema schriftlich Multiplizieren (mit und ohne Komma) verstanden zu haben? Möchtet ihr das Thema ein bisschen üben? Wir bieten euch hier die Möglichkeit Aufgaben zu rechnen und sich die Lösung dabei anzusehen. Fragen und Aufgaben können per Klick übersprungen werden. Wie lautet die Lösung dieser Aufgabe?

• 2134 · 2 = ?

• 2418
• 4268
• 4247
• 2143

Weiter zur Lösung » Aufgabe überspringen »

Du hast 0 von 5 Aufgaben erfolgreich gelöst.