Was ist ein Term? ▷ Beispiele und Vereinfachen

Eine sinnvolle mathematische Zeichenreihe wird in der Mathematik als Term bezeichnet. Beispiele für Terme und die Umformung von Termen mit Rechenregeln sehen wir uns hier an. Die Lerninhalte zu Termen gibt es als Text und als Video.

Wie in der Einleitung bereits erwähnt, ist ein Term eine mathematische Zeichenkette. Diese Kette muss sinnvoll sein. Die Zeichenkette ist zum Beispiel nicht sinnvoll wenn es eine geöffnete Klammer gibt, aber keine schließende Klammer. Terme gibt es mit und ohne Variablen (= Buchstaben).

Dies sind Terme:

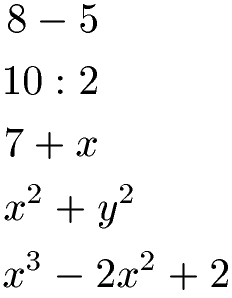
Ein Term darf keine Zeichen für gleich (=), größer (>) oder kleiner (<) beinhalten. In diesem Fälle würde es sich nicht um Terme, sondern um Gleichungen oder Ungleichungen handeln.

Wie werden Terme vereinfacht?

Im Mathematik-Unterricht geht es sehr oft darum Terme zu vereinfachen. Dabei werfen wir hier vor allem einen Blick auf Terme mit Variablen (= Buchstaben) und wie man diese vereinfacht. Denn insbesondere bei Termen mit Variablen tun sich viele Menschen bei der Berechnung sehr schwer.

Variablen sind Platzhalter. Diese Platzhalter werden eingesetzt wenn man die Zahl noch nicht kennt. In der Schule werden als Variablen oft a, b, x, y oder z verwendet. In Termen können Variablen vorkommen. Sind die Variablen gleich können diese oft zusammengefasst werden.

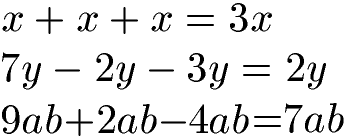
In einem Term können auch verschiedene Variablen vorkommen. Nur wenn alle Variablen jeweils gleich sind, darf zusammengefasst werden. Im nächsten Beispiel darf alles mit ab zusammengefasst werden und alles mit xy.

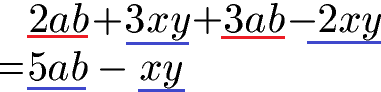
Zum besseren Verständnis noch ein weiteres Beispiel. Wichtig: x und xy dürfen nicht zusammengefasst werden, auch wenn in xy ein x vorkommt.

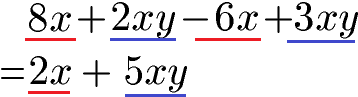
Welche Rechenregeln für Terme gelten sehen wir uns im nächsten Abschnitt an.

Anzeigen:

Welche Rechenregeln gelten für Terme?

Für Terme mit Variablen gelten genauso die Rechenregeln wie man sie von einfachen Aufgaben bzw. Termen ohne Variablen her kennt. Daher gehen wir diese einmal Stück für Stück durch. Die erste Regel lautet von links nach rechts. Kommen nur Addition und Subtraktion vor wird einfach von links nach rechts Stück für Stück durchgerechnet. Beispiel:

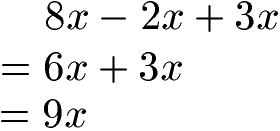
Die zweite Regel lautet Punkt vor Strich. Sie besagt, dass erst eine Multiplikation oder Division berechnet wird. Sind alle Multiplikationen und Divisionen berechnet wird im Anschluss addiert oder subtrahiert. Ein Beispiel:

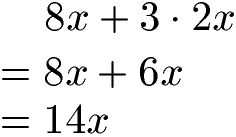
Hinweis: Steht zwischen der Zahl und der Variablen kein Zeichen wird immer von einer Multiplikation ausgegangen. So ist 14x nichts anderes als 14 · x.

Wie geht man mit Klammern bei Termen um?

In manchen Termen kommt eine Klammer vor. Eine Klammer wird immer zuerst berechnet. Im Beispiel 3x(2 + 3) wird daher erst der Inhalt der Klammer berechnet. Dieser ergibt 6. Im Anschluss wird noch mit der 3x vor der Klammer multipliziert. Die Rechnung:

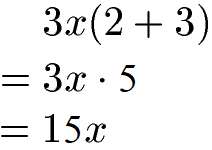
Es spielt keine Rolle, ob die Klammer am Anfang oder am Ende eines Terms steht. Der Inhalt einer Klammer wird zuerst berechnet, sofern dies möglich ist.

Im nächsten Beispiel geht dies nicht, da 3x + 4 nicht ausgerechnet werden kann ohne x zu kennen. Daher lösen wir die Klammer auf. Die Rechenregel bzw. das Rechengesetz dazu lautet Distributivgesetz. Dieses Gesetz besagt, dass jeder Teil innerhalb der Klammer mit der Zahl davor oder danach multipliziert wird. Genau dies passiert bei der Rechnung:

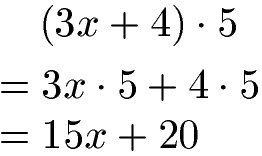
Die 15x + 20 können nicht weiter vereinfacht werden. Daher ist die Rechnung an dieser Stelle komplett.

Wie geht man mit Potenzen bei Termen um?

Potenzen können ebenfalls in Termen vorkommen. In der Mathematik wird erst eine Klammer berechnet, danach eine Potenz und im Anschluss Punkt vor Strich.

Im nächsten Beispiel haben wir eine Klammer mit dem Inhalt 3a. Diese Klammer wird hoch 2 genommen, sprich es liegt eine Potenz vor. Die 3a in der Klammer können wir nicht vereinfachen, daher rechnen wir die Potenz aus. Wir schreiben die Potenz aus, indem wir anstatt (3a)² nun (3a)(3a) schreiben. Dies rechnen wir aus: 3 · 3 = 9 und a · a = a². Danach vereinfachen wir die Rechnung noch einmal:

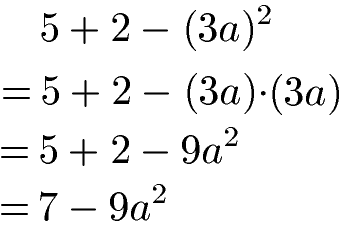
Wichtig: Es gibt einen Unterschied zwischen 3a² und (3a)². Bei 3a² wird nur das a quadriert, bei (3a)² hingegen wird 3a quadriert.