Potenzen verstehen: Basis und Exponent
Geschrieben von: Dennis RudolphDonnerstag, 10. Februar 2022 um 10:37 Uhr
Was sind Potenzen und wozu braucht man diese? Wie rechnet man bei Potenzen? Du lernst hier wie Potenzen aufgebaut sind, wie man mit positiven und negativen Potenzen rechnet und wozu du Zehnerpotenzen einsetzen kannst. Ich versuche die Inhalte so einfach zu erklären, wie ich dies selbst bei meiner Oma (lange aus der Schule raus) tun würde. Die Inhalte liegen als Text und als Video vor.
Was ist eine Potenz in der Mathematik? Potenzen sind Abkürzungen für die Multiplikation gleicher Zahlen. Ein Beispiel für eine Potenz:
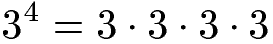
Potenzen bestehen aus einer Basis und einem Exponenten. Der Exponent wird dabei als kleinere Zahl rechts oberhalb der Basis geschrieben. Wird eine Potenz ausgerechnet bezeichnet man das Ergebnis als Potenzwert.
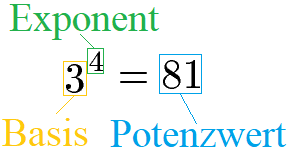
Die Basis wird in der Mathematik manchmal auch als Grundzahl bezeichnet. Der Exponent kann Alternativ auch Hochzahl genannt werden.
Für was braucht man Potenzen?
In der Mathematik werden Potenzen zum Beispiel für die Berechnung von Flächen und Volumen eingesetzt. Außerdem helfen sie dabei Multiplikationen abzukürzen. In den Grundlagen der Potenzrechnung geht es zunächst darum einfache Potenzen zu berechnen.
Zweierpotenzen berechnen:
Potenzen mit der Basis 2 werden als Zweierpotenzen bezeichnet. Beim Ausrechnen wird so oft die Zahl 2 geschrieben wie der Exponent dies vorsieht. Zwischen den 2ern werden dabei Malzeichen geschrieben. Die Potenz kann im Anschluss ausgerechnet werden.
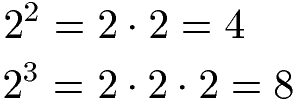
Viererpotenzen berechnen:
Bei den nächsten beiden Beispielen liegen Viererpotenzen vor. Auch bei diesen Potenzen wird die Basis so oft geschrieben wie die Hochzahl dies vorgibt. Zwischen die Wiederholungen der 4 wird das Zeichen für die Multiplikation geschrieben. Im Anschluss kann der Potenzwert berechnet werden.
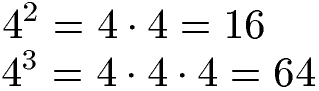
Potenzen mit Buchstaben (Variablen):
Potenzen können Variablen (= Buchstaben) beinhalten. Variablen werden verwendet wenn die Zahl noch nicht bekannt ist. Gleiche Variablen bedeuten dabei gleiche Zahlen. Im einfachsten Fall kommt die Variable in der Basis vor. Sie wird für die Multiplikation(en) so oft wiederholt wie der Exponent dies verlangt.
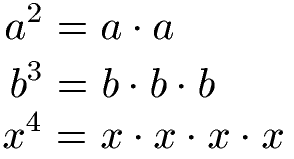
Anzeigen:
Was sind Zehnerpotenzen?
Zehnerpotenzen sind Potenzen mit der Basis 10. Die Zahl 10 wird so oft mit sich selbst multipliziert wie der Exponent vorgibt. Für die nächsten drei Beispiele werden natürliche Zahlen verwendet um Zehnerpotenzen zu finden.
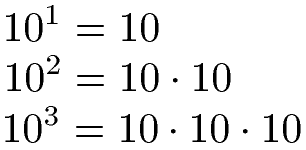
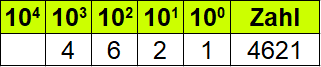
Zehnerpotenzen können mit der Hilfe einer Stellenwerttabelle bzw. Stellenwerttafel zerlegt werden. Im nächsten Beispiel wird die Zahl 4621 Stelle für Stelle in eine Tabelle eingetragen. Achtet dabei auf die Zehnerpotenzen von 100 bis 104 oberhalb.
Eine Dezimalzahl kann direkt als eine Summe aus Zehnerpotenzen geschrieben werden:
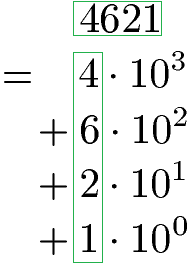
Eine solche Summe aus Zehnerpotenzen wird als Stufenform oder Stufendarstellung bezeichnet. Mehr zu diesem Thema findest du unter Zehnerpotenzen.
Wie berechnet man Potenzen mit negativer Basis?
Potenzen mit negativer Basis können ausmultipliziert werden, indem die negative Zahl so oft mit sich selbst multipliziert wird, wie dies im Exponenten vorgesehen ist. Um die einzelnen Faktoren werden dabei Klammern gesetzt. Dies dient zur Verdeutlichung einer Multiplikation negativer Zahlen (um eine Verwechselung durch Subtraktion zu vermeiden).
Potenz mit negativer Basis Beispiel 1:
Die Multiplikation von Potenzen mit negativer Basis führt zu einem negativen Potenzwert wenn der Exponent ungerade ist. Mit anderen Worten: Endet der Exponent auf 1, 3, 5, 7 oder 9 ist das Ergebnis der Berechnung eine negative Zahl. Im nächsten Beispiel ist der Potenzwert -8.
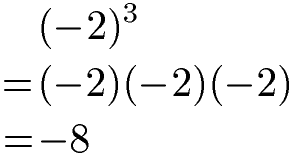
Potenz mit negativer Basis Beispiel 2:
Die Multiplikation von Potenzen mit negativer Basis führt zu einem positiven Potenzwert wenn der Exponent gerade ist. Mit anderen Worten: Endet der Exponent auf 0, 2, 4, 6 oder 8 ist das Ergebnis der Berechnung eine positive Zahl. Die nächste Aufgabe hat den Potenzwert +16.
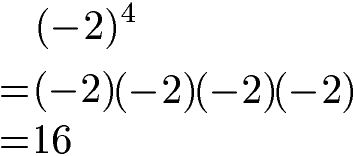
Was bedeutet der negative Exponent?
Potenzen mit negativen Exponenten dienen zur Darstellung sehr kleiner Zahlen. Der negative Exponent kann mit der Hilfe eines Bruchs in einen positiven Exponenten umgewandelt werden.
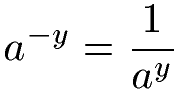
Die Potenz mit einer negativen Zahl im Exponenten wird zu einem Bruch mit 1 im Zähler und der gleichen Potenz mit umgekehrtem Vorzeichen im Nenner. So wird aus der Potenz 3-4 die Potenz 34 im Nenner bei 1 im Zähler. Aus 2-3 wird 23 im Nenner bei 1 im Zähler.
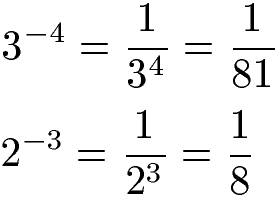
Da der Zähler 1 ist und der Nenner durch die positive Potenz sehr groß wird entstehen relativ kleine Zahlen.
Welche Potenzgesetze gibt es?
Potenzgesetze bzw. Potenzregeln dienen dazu Potenzen zu vereinfachen oder umzuformen. Potenzgesetze gibt es für alle Grundrechenarten (Addition, Subtraktion, Multiplikation und Division). Außerdem gibt es Potenzgesetze für Wurzeln und Brüche.
Für die Umformung von Klammern werden diese Gesetze eingesetzt sowie zum Umgang mit gleichen oder unterschiedlichen Basen und Exponenten. Umfangreicher behandelt wir dieses Thema unter Potenzgesetze (Potenzregeln).
Potenzgesetze Addition und Subtraktion:
Bei gleicher Basis und gleichem Exponenten können die Koeffizienten einfach addiert werden. Dies funktioniert sowohl für die Addition als auch für die Subtraktion.
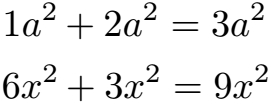
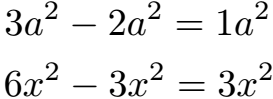
Soweit eine ganz kurze Einführung in die Gesetze zu Potenzen. Sehr ausführlich behandelt wir das Thema unter Potenzgesetze (Potenzregeln).
Wie berechnet man Zweierpotenzen?
Zweierpotenzen sind Potenzen mit der Basis 2. Die nächsten Beispiele zeigen 2er-Potenzen mit einem natürlichen Exponenten. Natürlich bedeutet, dass die Hochzahl eine natürliche Zahl (1, 2, 3, 4, 5, ...) ist. Die 2 kommt dabei so oft als Faktor vor wie der Exponent dies vorgibt.
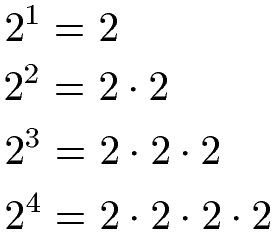
Zweierpotenzen können schriftlich sehr einfach berechnet werden, indem einfach alle Multiplikationen durchgeführt werden.
Meistgelesene Inhalte
- Allgemenbildung Quiz
- Prozentrechnung
- Bruchrechnen
- Satz des Pythagoras
- PQ-Formel
- Mitternachtsformel
- Polynomdivision
- Zinsrechnung
- Gleichungen umformen
- Nullstellen bestimmen
- Dreisatz
Neue Artikel
- Rationale Zahlen ▷ Ist eine Zahl rational?
- Bruch in Kommazahl (Dezimalzahl) umwandeln
- Koordinatensystem: Erklärung und Punkte
- Brüche kürzen und erweitern
- Brüche multiplizieren und dividieren
- Rechteck Eigenschaften: Flächeninhalt, Umfang und mehr
- Brüche addieren und subtrahieren
- Sachaufgaben Klasse 5 Mathematik
- Flächeninhalt Rechteck ▯ Beispiele + Erklärung
- Umfang Rechteck mit Formeln berechnen
