Primfaktorzerlegung und Primfaktoren

Welche Zahlen sind Primfaktoren? Wie zerlegt man in Primfaktoren? Und warum macht man eine Primfaktorzerlegung? Ich versuche die Inhalte so einfach zu erklären, wie ich dies selbst bei meiner Oma (lange aus der Schule raus) tun würde. Die Inhalte liegen als Text und als Video vor.

Bei einer Primfaktorzerlegung wird eine natürliche Zahl so weit es möglich ist zerlegt. Es entsteht eine Multiplikation möglichst kleiner Zahlen. Ein Beispiel:

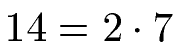
Dies ist bereits eine vollständige Zerlegung der Zahl 14. Die 2 und die 7 sind Primzahlen und können nicht weiter zerlegt werden. Da diese Primzahlen in einer Multiplikation vorkommen, werden die 2 und die 7 als Primfaktoren bezeichnet. Wir halten fest: Primfaktoren sind Primzahlen bei einer Multiplikation.

Wie macht man eine Primfaktorzerlegung?

Bei einer Primfaktorzerlegung suchst du einfache Teiler einer größeren Zahl. Dazu solltest du die Teilbarkeitsregeln mindestens bis zur Zahl 10 kennen. Ist eine Zahl gerade (endet auf 0, 2, 4, 6 oder 8) ist diese durch 2 ohne Rest teilbar.

Als einfache Erklärung sehen wir uns die Primfaktorzerlegung der Zahl 64 an. Die 64 zerlegen wir erst in 2 · 32 und diese 32 zerlegen wir erneut bis wir am Ende nur eine Multiplikation vieler 2er haben. Da wir 6 Mal die Zahl 2 haben können wir dies als Potenz mit 2⁶ schreiben.

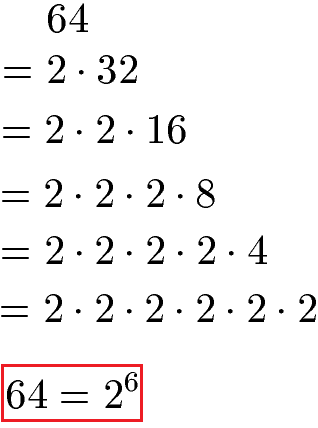
Im Zahlenraum bis 100 ist es meistens recht einfach durch die Teilbarkeitsregeln die Zahl in Primfaktoren zu zerlegen.

Anzeigen:

Wie zerlegt man in Primfaktoren?

Die Zahl 140 kann ebenfalls in Primfaktoren zerlegt werden. Da die Zahl auf 0 endet können wir sie sehr einfach durch 10 teilen und erhalten 140 = 10 · 14. Die 10 und die 14 können wir ebenfalls sehr einfach in eine Multiplikation zweier Zahlen zerlegen. Wir erhalten die Primzahlen 2, 5 und 7.

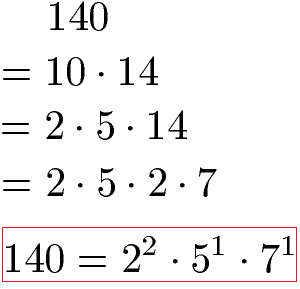
Die 2 · 5 · 2 · 7 können noch in eine Potenzschreibweise gebracht werden: Die 2 kommt doppelt vor, daher im Anschluss die Potenz 2². Die 5 und die 7 kommen nur ein einziges Mal vor, daher 5¹ und 7¹.

Zwei Anwendungen der Primfaktorzerlegung sind das kleinste gemeinsame Vielfache und der größte gemeinsame Teiler. Im nächsten Abschnitt sehen wir uns dazu ein Beispiel an.

Warum macht man eine Primfaktorzerlegung?

Die Primfaktorzerlegung dient dazu das kleinste gemeinsame Vielfache (kgV) und den größten gemeinsamen Teiler (ggT) einer natürlichen Zahl zu finden. Als Beispiel sollen kgV und ggT der Zahlen 99 und 351 berechnet werden. Dazu zerlegen wir zunächst die 99 in die Primfaktoren und fassen diese im Anschluss als Potenz zusammen.

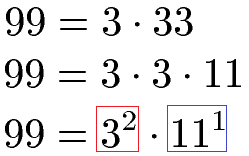
Außerdem müssen wir die Zahl 351 in Multiplikationen aus Primzahlen zerlegen. Dies bringt uns 3 · 3 · 3 · 13 als Ergebnis. Wir fassen die Primfaktoren in Potenzschreibweise zusammen.

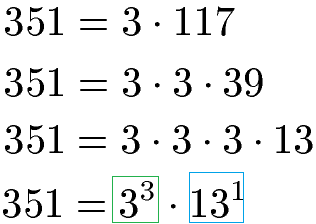
Den größten gemeinsamen Teiler (ggT) finden wir, indem wir die Primfaktoren suchen welche in beiden Zerlegungen vorkommen und den kleinsten Exponenten haben. Die Basis 3 kommt in 3² und 3³ vor. Wir nehmen die kleinere Potenz mit 3². Die anderen Basen (11 und 13) kommen nur in einer der beiden Zerlegungen vor und fallen daher raus. Wir erhalten das ggT mit 3² = 9.

Das kleinste gemeinsame Vielfache (kgV) finden wir, indem wir jede Potenz aus beiden Zerlegungen nehmen und jeweils den höchsten Exponenten suchen. Die Basis 3 kommt in 3² und 3³ vor. Wir nehmen die größere Potenz mit 3³. Die Basen 11 und 13 kommen nur jeweils bei einer Zerlegung vor und werden daher jeweils übernommen. Das kgV lautet damit 3³ · 11¹ · 13¹ = 3861.

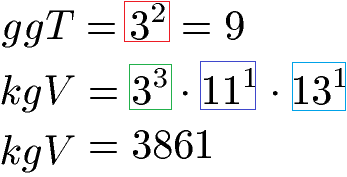
Ich empfehle dir noch die Inhalte unter kleinstes gemeinsames Vielfaches (kgV) und größter gemeinsamer Teiler (ggT).