Größter gemeinsamer Teiler (ggT) mit Beispielen

Was ist der größte gemeinsame Teiler (ggT)? Wie berechne ich den größten gemeinsamen Teiler? Zwei Verfahren zur Berechnung stelle ich dir mit der Teilermenge und der Primfaktorzerlegung vor. Ich versuche die Inhalte so einfach zu erklären, wie ich dies selbst bei meiner Oma (lange aus der Schule raus) tun würde. Die Inhalte liegen als Text und als Video vor.

Der größte gemeinsame Teiler (ggT) ist die größte natürliche Zahl, durch die du zwei oder mehr Zahlen teilen kannst. Um diesen größten gemeinsamen Teiler zu berechnen, sehen wir uns zunächst die Teilermenge an und wie man aus dieser das ggT abliest. Als Beispiel findest du hier die Teilermengen der Zahlen 36 und 48.

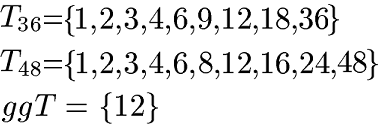
Das größte gemeinsame Teiler ist die größte Zahl welche in beiden Mengen auftritt. Dies ist hier die Zahl 12. Wir erhalten ggT(36,48) = 12. Solltest du Probleme haben die Teiler einer Zahl zu finden kannst du gerne noch einmal in die Inhalte unter Teiler und Vielfache reinsehen. Ebenfalls hilfreich sind die Teilbarkeitsregeln.

Größter gemeinsamer Teiler durch Primfaktorzerlegung

Bei großen Zahlen ist es schwierig alle Teiler schnell zu berechnen. Ohne die Teiler lässt sich jedoch nicht der größte gemeinsame Teiler finden. Eine Lösung dieses Problems stellt die Primfaktorzerlegung dar. Dabei zerlegt man eine Zahl in eine Multiplikation möglichst kleiner Faktoren (= Primzahlen).

Beispiel: Gesucht ist der größte gemeinsame Teiler der Zahlen 351 und 99. Wir zerlegen die 351 in eine Multiplikation möglichst kleiner Zahlen. Dies sind hier 3 Mal die 3 und 1 Mal die 13. Dies können wir auch in Form einer Potenz schreiben.

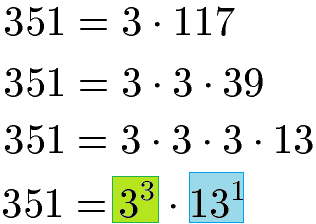
Ebenso zerlegen wir die 99 in Primfaktoren. Wir erhalten die Zahl 3 insgesamt 2 Mal und die 11 nur ein Mal. Auch dies schreiben wir in Form einer Potenz.

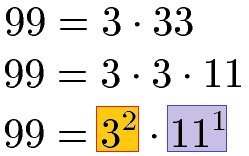
Wir sehen uns nun alle Potenzen genauer an und wählen die Potenzen, welche in beiden Zerlegungen vorkommen. Die 11 und die 13 kommen nur bei einer der beiden Zerlegungen vor und fallen daher raus. Die Basis 3 mit 3³ und 3² kommt in beiden Zerlegungen vor und ist daher für uns wichtig. Wir nehmen jedoch nur die kleinere Potenz.

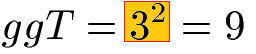
Der kleinste gemeinsame Teiler von 99 und 351 ist die Zahl 9.

Anzeigen:

Berechne ggT für 3 Zahlen

Der größte gemeinsame Teiler für 3 Zahlen lässt sich ebenfalls mit der Primfaktorzerlegung suchen. Für das Beispiel soll der größte gemeinsame Teiler der Zahlen 198, 144 und 88 gesucht werden. Wir führen eine Primfaktorzerlegung der drei Zahlen durch und schreiben diese in der Potenzschreibweise.

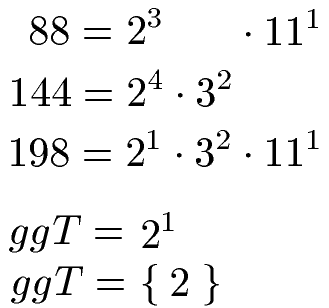
Die Potenzen mit der Basis 3 und 11 gibt es nicht bei allen Zerlegungen und fallen daher raus. Nur die Basis 2 kommt in allen Zerlegungen vor mit 2³, 2⁴ und 2¹. Wir nehmen die kleinste Potenz davon, sprich 2¹. Das ggT ist damit 2¹ = 2.

Als nächste Themen empfehle ich dir noch einen Blick auf das kleinste gemeinsame Vielfache (kgV) und die Primfaktorzerlegung.