Rechengesetze verstehen: kommutativ, assoziativ und distributiv

Welche Rechengesetze gibt es? Wie funktionieren Kommutativgesetz, Assoziativgesetz und Distributivgesetz? Welche Formeln müssen verwendet werden und worauf muss man achten? Ich versuche alles so einfach zu erklären, wie ich dies selbst bei meiner Oma (lange aus der Schule raus) tun würde.

Es gibt vier Rechengesetze und eine ganz wichtige Rechenregel, die jeder kennen sollte. Dies sind:

• Das Kommutativgesetz für die Addition und Multiplikation.
• Das Assoziativgesetz für die Addition und Multiplikation.
• Das Distrubutivgesetz mit allen Grundrechenarten.
• Die Regel Punkt vor Strich um die Rechengesetze auch ausrechnen zu können.

Zur Punktrechnung vor Strichrechnung findest du Erklärungen als Text und Video unter Punkt vor Strich. Die drei Rechengesetze sehen wir uns gleich hier an.

Wie geht das Kommutativgesetz (1. Rechengesetz)?

Das Kommutativgesetz sagt aus, dass es keine Rolle für das Ergebnis spielt, in welcher Reihenfolge Zahlen stehen. Das Kommutativgesetz gilt für die Addition und die Multiplikation. Für die Subtraktion und die Division gilt das Kommutativgesetz hingegen nicht. Das Kommutativgesetz gilt als 1. Rechengesetz.

Kommutativgesetz Addition Gleichung und Beispiel:

Die Reihenfolge der Zahlen bei einer Addition kann beliebig vertauscht werden ohne das sich das Ergebnis verändert.

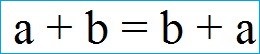
Die Reihenfolge der Zahlen (Summanden) spielt keine Rolle. Ob 4 + 8 oder 8 + 4 gerechnet wird, die Summe ist jeweils 12.

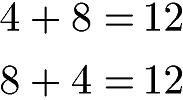
Kommutativgesetz Multiplikation Gleichung und Beispiel:

Die Reihenfolge der Zahlen bei einer Multiplikation kann beliebig vertauscht werden ohne das sich das Ergebnis verändert.

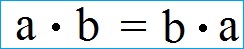
Es ist egal, ob die 5 mit der 3 oder die 3 mit der 5 multipliziert wird. Das Produkt ist stets 15.

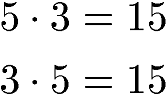
Das Kommutativgesetz gilt nicht für die Subtraktion oder Division. Bei diesen beiden Grundrechenarten darf die Reihenfolge der Zahlen nicht vertauscht werden, sonst entsteht ein anderes Ergebnis. Weitere Beispiele und Erklärungen zu diesem Rechengesetz findest du unter Kommutativgesetz.

Anzeigen:

Wie geht das Assoziativgesetz (2. Rechengesetz)?

Das Assoziativgesetz besagt, dass die Reihenfolge von 3 Zahlen (oder mehr) bei einer Addition für das Ergebnis keine Rolle spielt. Das Assoziativgesetz sagt außerdem aus, dass die Reihenfolge von 3 Zahlen (oder mehr) bei einer Multiplikation für das Ergebnis keine Rolle spielt. Für die Subtraktion und Division gilt das Assoziativgesetz hingegen nicht. Das Assoziativgesetz gilt als 2. Rechengesetz.

Assoziativgesetz Addition Gleichung und Beispiel:

Es spielt für das Ergebnis einer Berechnung keine Rolle in welcher Reihenfolge Zahlen bei einer Addition stehen.

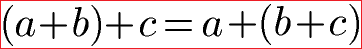
Die natürlichen Zahlen 1, 2 und 3 können in beliebiger Reihenfolge addiert werden. Durch das Setzen von Klammern kann die Reihenfolge der Berechnung verändert werden. Hinweis: Klammern werden zuerst berechnet. Die Summe bleibt in allen Fällen gleich.

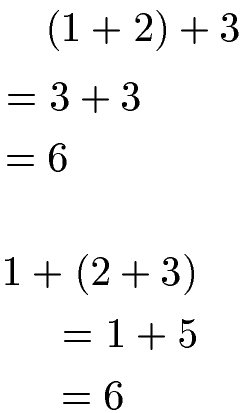
Die drei Zahlen können für die Länge von Strecken stehen. So können drei Strecken in beliebiger Reihenfolge aneinander gereiht werden. Die Gesamtlänge ist jeweils gleich lang.

Assoziativgesetz Multiplikation Gleichung und Beispiel:

Es spielt für das Ergebnis einer Multiplikation keine Rolle in welcher Reihenfolge die Zahlen stehen oder multipliziert werden.

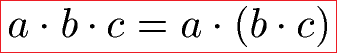
Die natürlichen Zahlen 3, 4 und 5 können in beliebiger Reihenfolge multipliziert werden. Am Ergebnis 60 ändert sich dabei nichts.

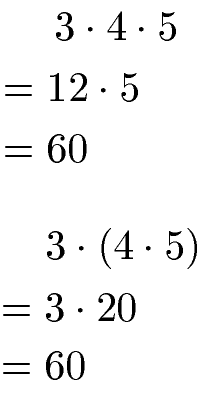
Das Assoziativgesetz gilt nicht für die Subtraktion oder Division. Bei diesen beiden Grundrechenarten darf die Reihenfolge der Zahlen nicht vertauscht werden, sonst entsteht ein anderes Ergebnis. Weitere Beispiele und Erklärungen zu diesem Rechengesetz findest du unter Assoziativgesetz.

3. Rechengesetz: Was ist das Distributivgesetz (3. Rechengesetz)?

Das Distributivgesetz wird dazu verwendet Terme in der Mathematik umzuformen. Klammern können aufgelöst werden. Gemeinsame Zahlen oder Variablen können ausgeklammert werden. Das Distributivgesetz kann als 3. Rechengesetz bezeichnet werden.

Distributivgesetz Addition Gleichung und Beispiel:

Zum Auflösen oder Erzeugen von Klammern gelten diese beiden Gleichungen.

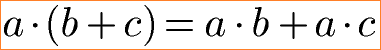
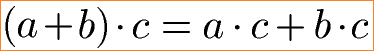
Bei einer Rechenaufgabe soll eine Klammer mit dem Distributivgesetz aufgelöst werden. Dazu wird die Zahl vor der Klammer mit jedem Summanden in der Klammer einzeln multipliziert. Nach dem Auflösen der Klammer muss die Rechenregel Punkt vor Strich beachtet werden. Daher werden zunächst beide Multiplikationen ausgerechnet und erst im Anschluss die Addition.

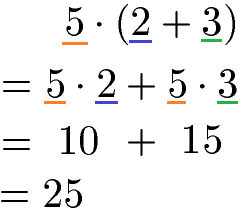
Distributivgesetz Subtraktion Gleichung und Beispiel:

Zum Auflösen oder Erzeugen von Klammern gelten diese beiden Gleichungen.

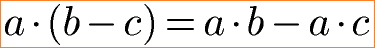
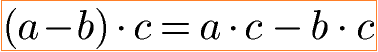
Als Beispiel gibt es eine Klammer mit einer Differenz. Die Zahl vor der Klammer wird mit der 3 und mit der 1 multipliziert. Dazwischen kommt - wie in der allgemeinen Gleichung auch - ein Minuszeichen. Zum besseren Verständnis werden dabei Farben unter den Zahlen eingesetzt. Beachtet auch hier Punkt vor Strich.

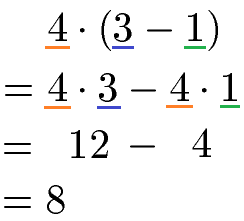
Distributivgesetz Multiplikation Klammer erzeugen mit Formel und Beispiel:

Mit der Formel zum Distributivgesetz lassen sich gemeinsame Zahlen oder Variablen ausklammern.

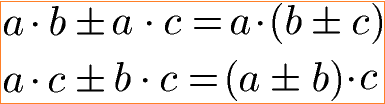
Im nächsten Beispiel kommt die 2 bei beiden Multiplikationen jeweils vor und darf daher vor die Klammer gezogen werden.

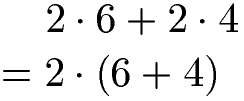
Distributivgesetz Formel zur Division mit Beispiel:

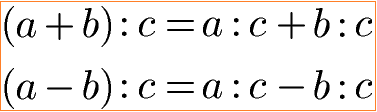
Die Klammer enthält 20 + 10 und diese Klammer soll durch 5 geteilt werden. Sie kann aufgelöst werden in dem jeder Summand innerhalb der Klammer durch die 5 geteilt wird.

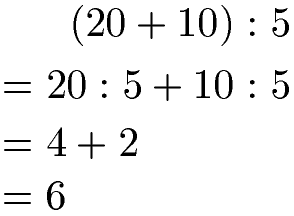
Weitere Beispiele und Erklärungen zu diesem Rechengesetz findest du unter Distrubutivgesetz.