Rechenmauer (Zahlenmauer) Erklärung

Was ist eine Zahlenmauer bzw. Rechenmauer? Wie löst man eine Rechenmauer? Was muss ich beachten wenn Steine weiter unten leer sind? Diese Antworten bekommst du hier. Ich versuche alles so einfach zu erklären, wie ich dies selbst bei meiner Oma (lange aus der Schule raus) tun würde. Die Inhalte liegen als Text und als Video vor.

Eine Rechenmauer - auch Zahlenmauer genannt - besteht aus Steinen, in welche Zahlen geschrieben werden. Solch eine Mauer hat mindestens 2 Steine in der untersten Reihe, sprich mindestens 2 Grundsteine. In der Grundschule werden Zahlenmauern eingesetzt um Addition (+) und Subtraktion (-) von Zahlen zu üben. Die nächsten beiden Grafiken zeigen Rechenmauern mit 2 oder 3 Grundsteinen.

Rechenmauer mit 2 Grundsteinen (noch ohne Zahlen):

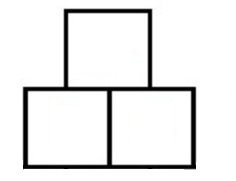
Rechenmauer mit 3 Grundsteinen (noch ohne Zahlen):

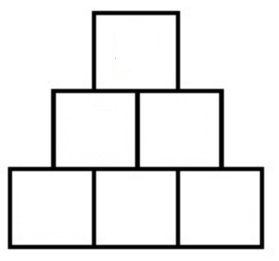
In den nächsten Abschnitten sehen wir uns Beispiele zum Lösen von Rechenmauern an.

Beispiele Rechenmauer Klasse 1 und 2

Bei einer Zahlenmauer findet sich im Stein oberhalb zweier anderer Steine die Summe. Dies klingt kompliziert, ist jedoch eigentlich ganz einfach. Als Beispiel nehmen wir eine Rechenmauer mit 8 und 6 in den Grundsteinen. Der Stein darüber erhält die Zahl 14, denn 8 + 6 = 14.

Beispiel 1: Rechenmauer

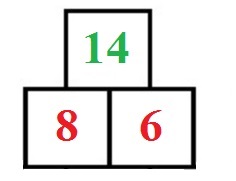
In der 1. Klasse wird die Rechenmauer oft im Zahlenraum bis 10 behandelt. In späteren Klassenstufen werden die Zahlen größer. Es spielt keine Rolle, ob die Zahlen größer werden oder die Rechenmauer mehr Steine aufweist. Stets hat der Stein darüber die Summe der Steine darunter.

Beispiel 2: Zahlenmauer mit 3 Steinen

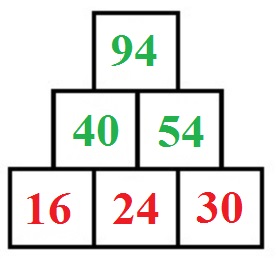
Wir haben eine Zahlenmauer mit den Zahlen 16, 24 und 30 in den Grundsteinen. Welche Zahlen müssen in die Steine darüber geschrieben werden?

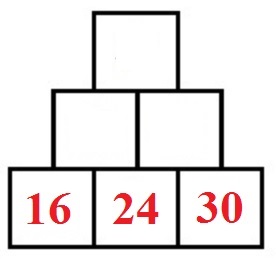
Lösung:

• Wir rechnen zunächst die 2. Reihe aus:
  • 16 + 24 = 40
  • 24 + 30 = 54
• Danach rechnen wir den obersten Stein aus:
  • 40 + 54 = 94

Anzeigen:

Wie funktioniert eine Zahlenmauer mit Subtraktion?

Sind Steine weiter unten leer, dann findet man deren Zahlen durch eine Subtraktion. Zur Erinnerung: Die Subtraktion (-) ist die Umkehrung der Addition (+).

Beispiel 3: Zahlenmauer und Subtraktion

Wir haben eine Zahlenmauer bei der nicht alle Grundsteine Zahlen enthalten. Welche Zahlen müssen eingetragen werden um die Rechenmauer vollständig auszufüllen?

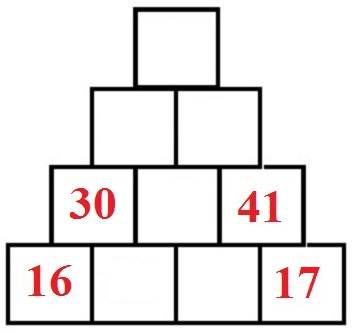
Zunächst berechnen wir die unterste Reihe:

• 30 - 16 = 14 für die unterste Reihe (zweiter Stein).
• 41 - 17 = 24 für die unterste Reihe (dritter Stein).

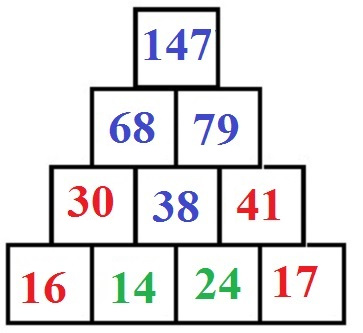
Wurden die Steine in der unterste Reihe berechnet, kann durch Additionen (+) der Rest berechnet werden.

• 14 + 24 = 38
• 30 + 38 = 68
• 38 + 41 = 79
• 68 + 79 = 147

Aufgaben / Übungen Rechenmauer

In diesem Abschnitt kannst du das Thema "Zahlenmauer" einmal selbst üben.

Aufgabe 1:

• Welche Zahl muss in den obersten Stein geschrieben werden?

• 4
• 10
• 9
• 5

Weiter zur Lösung » Aufgabe überspringen »

Du hast 0 von 4 Aufgaben erfolgreich gelöst.

Rechenmauer: Weiterführende Inhalte